
在平面直角坐标系xOy中,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,4),D为OC的中点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,4),D为OC的中点.
(1)求m的值;
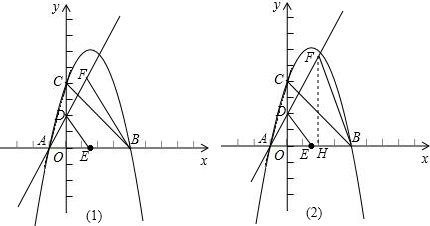
(2)抛物线的对称轴与 x轴交于点E,在直线AD上是否存在点F,使得以点A、B、F为顶点的三角形与△ADE 相似?若存在,请求出点F的坐标,若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点G,使△GBC中BC边上的高为 ?若存在,求出点G的坐标;若不存在请说明理由.
?若存在,求出点G的坐标;若不存在请说明理由.
(1)-1;(2)(1,4)或(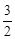 ,5);(3)(
,5);(3)(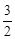 ,
,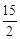 )或(
)或(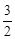 ,
,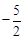 ).
).
解析试题分析:(1)由抛物线 与y轴交于点C(0,4),把C点的坐标代入解析式建立方程,求出方程的解,就可以求出m的值;
与y轴交于点C(0,4),把C点的坐标代入解析式建立方程,求出方程的解,就可以求出m的值;
(2)先求出抛物线与x轴的交点坐标,根据抛物线的对称性求出E点的坐标,然后根据对应角不同的情况就可以求出F的不同坐标;
(3)先由待定系数法求出直线BC的解析式,然后由题目的条件求出与直线BC平行且距离为 的直线的解析式,再由抛物线的对称轴与这些与BC平行的直线的解析式构建方程组求出其解,就可以求出G的坐标.
的直线的解析式,再由抛物线的对称轴与这些与BC平行的直线的解析式构建方程组求出其解,就可以求出G的坐标.
试题解析:(1)抛物线 与y轴交于点C(0,4),
与y轴交于点C(0,4),
∴5+m=4.∴m=-1.
(2)抛物线的解析式为 y=-x2+3x+4.
可求抛物线与x轴的交点A(-1,0),B(4,0).
可求点E的坐标(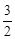 ,0).
,0).
由图知,点F在x轴下方的直线AD上时,△ABF是钝角三角形,不可能与△ADE相似,所以点F一定在x轴上方.
此时△ABF与△ADE有一个公共角,两个三角形相似存在两种情况:
当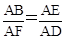 时,由于E为AB的中点,此时D为AF的中点,可求 F点坐标为(1,4).
时,由于E为AB的中点,此时D为AF的中点,可求 F点坐标为(1,4).
②当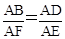 时,
时, ,解得:
,解得: 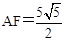 .
.
如图(2)过F点作FH⊥x轴,垂足为H.
∴ .
.
∵D是OC的中点,∴OD=2.
∴由勾股定理得: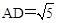 .
.
∴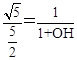 , 解得
, 解得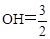 .
.
由勾股定理得: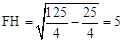 ,
,
∴F的坐标为(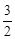 ,5).
,5).
(3)在抛物线的对称轴上存在符合题意的点G.
由题意,可知△OBC为等腰直角三角形,直线BC为y=-x+4.
如图(3),
∵MQ∥BC,QP= ,∴由勾股定理,得CQ=5.
,∴由勾股定理,得CQ=5.
∴可求与直线BC平行且距离为 的直线为y=-x+9或y=-x-1.
的直线为y=-x+9或y=-x-1.
∴点G在直线y=-x+9或y=-x-1上.
∵抛物线的对称轴是直线x=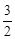 ,
,
∴ 或
或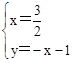 ,解得:
,解得: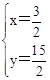 或
或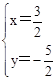 .
.
∴点G的坐标为(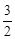 ,
,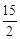 )或(
)或(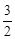 ,
,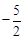 ).
).

考点:1.二次函数综合题;2.两条直线相交或平行问题;3.待定系数法求二次函数解析式;4.等腰直角三角形的性质;5.相似三角形的判定和性质;6.分类思想的应用.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
已知一个二次函数的顶点A的坐标为(1,0),且图像经过点B(2,3).
(1)求这个二次函数的解析式.
(2)设图像与y轴的交点为C,记 ,试用
,试用 表示
表示 (直接写出答案)
(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
抛物线 经过点A(4,0),B(2,2),连结OB,AB.
经过点A(4,0),B(2,2),连结OB,AB.
(1)求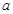 、
、 的值;
的值;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转l35°得到△OA′B′,写出A′B′的中点P的出标.试判断点P是否在此抛物线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣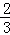 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,某中学校园有一块长为35m,宽为16m的长方形空地,其中有一面已经铺设长为26m的篱笆围墙,学校设计在这片空地上,利用这面围墙和用尽已有的可制作50m长的篱笆材料,围成一个矩形花园或围成一个半圆花园,请回答以下问题:
(1)能否围成面积为300m2的矩形花园?若能,请写出其中一种设计方案,若不能,请说明理由.
(2)若围成一个半圆花园,则该如何设计?请写出你的设计方案.(π取3.14)
(3)围成的各种设计中,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与x轴交于点A(—2,0),交y轴于点B(0,
与x轴交于点A(—2,0),交y轴于点B(0, ).直
).直 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.
(1)求抛物线 与直线
与直线 的解析式;
的解析式;
(2)设点P是直线AD下方的抛物线上一动点(不与点A、D重合),过点P作 y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m与x的函数关系式,并求出m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线 (
( ).
).
(1)求抛物线与 轴的交点坐标;
轴的交点坐标;
(2)若抛物线与 轴的两个交点之间的距离为2,求
轴的两个交点之间的距离为2,求 的值;
的值;
(3)若一次函数 的图象与抛物线始终只有一个公共点,求一次函数的解析式.
的图象与抛物线始终只有一个公共点,求一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com