
【题目】如图,在△ABC中,AB=AC=3,∠B=50°,点D在线段BC上运动(不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.

(1)当∠BDA=105°时,∠BAD= °,∠DEC= °;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.
【答案】(1)25,105;(2)见解析;(3)当△ADE是等腰三角形时,∠BDA的度数为100°或115°.
【解析】
(1)利用邻补角的性质、等边对等角和三角形内角和定理解题即可;
(2)利用∠DEC+∠EDC=130°,∠ADB+∠EDC=130°,求出∠ADB=∠DEC,再利用AAS即可得出△ABD≌△DCE;
(3)根据等腰三角形的腰的情况分类讨论,在利用等腰三角形的性质和三角形的外角即可分别求出∠BDA.
解:(1)∵在△BAD中,∠B=∠50°,∠BDA=105°,∠ADE=50°,
∴∠BAD=180°﹣∠B﹣∠BDA=25°,∠EDC=180°﹣∠BDA﹣∠ADE=25°
∵AB=AC,
∴∠B=∠C=50°,
∴∠DEC=180°﹣∠C﹣∠EDC=180°﹣50°﹣25°=105°,
故答案为:25,105;
(2)∵∠B=∠C=50°,
∴∠DEC+∠EDC=180°﹣∠C=130°,
又∵∠ADE=50°,
∴∠ADB+∠EDC=180°﹣∠ADE =130°,
∴∠ADB=∠DEC,
在△ABD和△DCE中,
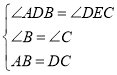
∴△ABD≌△DCE(AAS).
(3)当△ADE是等腰三角形时,∠BDA的度数为100°或115°,
①当ED=EA时,
∴∠DAE=∠EDA=50°,
∴∠BDA=∠C+DAE=100°;
②当DA=DE时,
∴∠DAE=∠DEA=![]() (180°﹣∠ADE)=65°,
(180°﹣∠ADE)=65°,
∴∠BDA=∠C+DAE=115°,
③当AD=AE时,
∠ADE=∠AED=50°
∵∠C=50°
∠AED是△EDC的外角
∴∠AED>∠C,与∠AED=50°矛盾
所以此时不成立;
综上所述:当△ADE是等腰三角形时,∠BDA的度数为100°或115°.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧![]() 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
⑴求证:AC=CD.
⑵若OB=2,求BH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学老师布置了这样一道作业题:
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧.BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
小聪提供了研究:先从特殊问题开始研究:当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′,然后利用α=90°,β=30°以及等边三角形的相关知识可解决这个问题.
(1)请结合小聪研究,画出当α=90°,β=30°时相应的图形;
(2)请结合小聪研究,求出当α=90°,β=30°时∠ADB的图形;
(3)请结合小聪研究,请解决数学老师布置的这道作业题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与
的图像与![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,且点
,且点![]() 的横坐标为
的横坐标为![]() .
.
(1)求![]() 的值与
的值与![]() 的长;
的长;
(2)若点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,D是AB的中点,M是边AC上一点,连接DM,以DM为直角边作等腰直角三角形DME,斜边DE交线段CM于点F,若S△MDF=2S△MEF,则CM的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com