
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
 如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
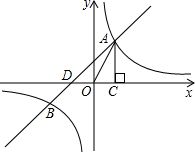 如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$(k1>0)与一次函数y2=k2x+1(k2≠0)的图象交于A,B两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC.
如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$(k1>0)与一次函数y2=k2x+1(k2≠0)的图象交于A,B两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 算筹是我国古代的计算工具之一,也是中华民族智慧的结晶,如图1中用算筹表示的算式是“7408+2366”,则图2中算筹表示的算式的运算结果为-426.
算筹是我国古代的计算工具之一,也是中华民族智慧的结晶,如图1中用算筹表示的算式是“7408+2366”,则图2中算筹表示的算式的运算结果为-426.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com