
 =
= ="6" …………………(2分)
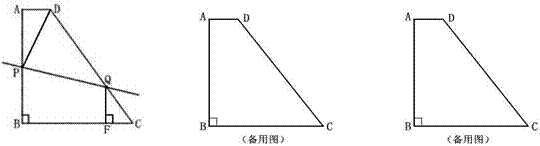
="6" …………………(2分)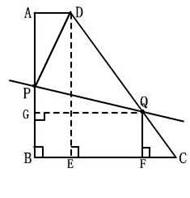 ∵DE⊥BC,QF⊥CB
∵DE⊥BC,QF⊥CB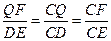
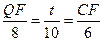 ∴CF=
∴CF=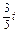 ,QF=
,QF=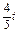 ,
,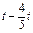 =
=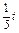 ,QG=8-
,QG=8-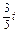
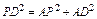 =(8-t)2+22=t2+16t+68,
=(8-t)2+22=t2+16t+68,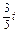 )2+(
)2+(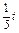 )2=
)2=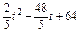
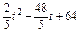 ,
,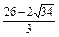 ,t2=
,t2=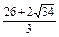 >8(舍去),
>8(舍去),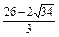 ; ………………(8分)
; ………………(8分)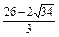 或8≤t<10时,以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形. 解析:
或8≤t<10时,以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形. 解析:

科目:初中数学 来源: 题型:
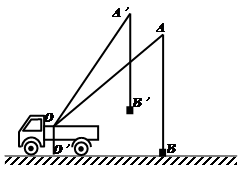
.(本题10分) 小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不
变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.且cosA=![]() ,sinA′=
,sinA′=![]() .
.
1.(1) 求此重物在水平方向移动的距离及在竖直方向移动的距离;
2.(2) 若这台吊车工作时吊杆最大水平旋转角度为120°,吊杆与水平线的倾角可以从30°转到60°,求吊车工作时,工作人员不能站立的区域的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
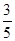 ,sinA′=
,sinA′=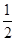 .
.
查看答案和解析>>
科目:初中数学 来源:2012届江苏省泰兴市济川中学九年级上学期期末考试数学卷 题型:解答题
.(本题10分) 小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不
变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.且cosA= ,sinA′=
,sinA′= .
.
【小题1】(1) 求此重物在水平方向移动的距离及在竖直方向移动的距离;
【小题2】(2) 若这台吊车工作时吊杆最大水平旋转角度为120°,吊杆与水平线的倾角可以从30°转到60°,求吊车工作时,工作人员不能站立的区域的面积。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省镇江市八年级上学期期末考试数学试卷(带解析) 题型:解答题
(本题10分)
在向红星镇居民介绍王家庄位置的时候,我们可以这样说:如图,在以红星镇为原点,正东方向为x轴正方向,正北方向为y轴正方向的平面直角坐标系(1单位长度表示的实际距离为1km)中,王家庄的坐标为(5,5);也可以说,王家庄在红星镇东北方向 km的地方。
km的地方。
还有一种方法广泛应用于航海、航空、气象、军事等领域。如右下图:在红星镇所建的雷达站O的雷达显示屏上,把周角每15°分成一份,正东方向为0°,相邻两圆之间的距离为1个单位长度(1单位长度表示的实际距离为1km),现发现2个目标,我们约定用(10,15°)表示点M在雷达显示器上的坐标,则:
(1)点N可表示为 ;王家庄位置可表示为 ;点N关于雷达站点0成中心对称的点P的坐标为 ;
(2)S△OMP= ;
(3)若有一家大型超市A在图中(4,30°)的地方,请直接标出点A,并将超市A与雷达站O连接,现准备在雷达站周围建立便民服务店B,使得△ABO为底角30°的等腰三角形,请直接写出B点在雷达显示屏上的坐标.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省镇江市八年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题10分)
在向红星镇居民介绍王家庄位置的时候,我们可以这样说:如图,在以红星镇为原点,正东方向为x轴正方向,正北方向为y轴正方向的平面直角坐标系(1单位长度表示的实际距离为1km)中,王家庄的坐标为(5,5);也可以说,王家庄在红星镇东北方向 km的地方。
km的地方。

还有一种方法广泛应用于航海、航空、气象、军事等领域。如右下图:在红星镇所建的雷达站O的雷达显示屏上,把周角每15°分成一份,正东方向为0°,相邻两圆之间的距离为1个单位长度(1单位长度表示的实际距离为1km),现发现2个目标,我们约定用(10,15°)表示点M在雷达显示器上的坐标,则:

(1)点N可表示为 ;王家庄位置可表示为 ;点N关于雷达站点0成中心对称的点P的坐标为 ;
(2)S△OMP= ;
(3)若有一家大型超市A在图中(4,30°)的地方,请直接标出点A,并将超市A与雷达站O连接,现准备在雷达站周围建立便民服务店B,使得△ABO为底角30°的等腰三角形,请直接写出B点在雷达显示屏上的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com