
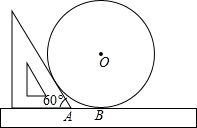
 如图,直尺、三角尺都和圆O相切,AB=8cm.求圆O的直径.
如图,直尺、三角尺都和圆O相切,AB=8cm.求圆O的直径.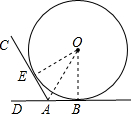 连接OE、OA、OB,
连接OE、OA、OB, ∠BAC,
∠BAC, ×120°=60°,
×120°=60°, =
=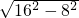 =8
=8 (cm),
(cm), cm,
cm, cm,
cm, cm.
cm. ∠BAC,求出∠BAC,求出∠OAB和∠BOA,求出OA,根据勾股定理求出OB即可.
∠BAC,求出∠BAC,求出∠OAB和∠BOA,求出OA,根据勾股定理求出OB即可.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com