

分析 先证明△ACD∽△ABE得到BE:CD=3:1得BE=18,再证明AF⊥BE即可求出BF的长.
解答 解:连接AF.
∵△ADE是由△ACB旋转得到,
∴∠CAD=∠BAE,
∵AC=AD,AB=AE,
∴∠ACD=∠C,∠ABE=∠AEB,
∵2∠ACD+∠CAD=180°,2∠ABE+∠BAE=180°,
∴∠ACD=∠ABE,
∴△ACD∽△ABE,
∴$\frac{AC}{AE}=\frac{CD}{BE}$,∠ACO=∠ABF,
∵AB=3AC,CD=6,
∴BE=18.
∵∠ACO=∠ABF,
∴四边形AFBC四点共圆,
∴∠AFE=∠BCA=90°,
∴AF⊥BE
∵AB=AE,
∴BF=$\frac{1}{2}$BE=9.
故答案为9.
点评 本题考查了旋转的性质、相似三角形的判定和性质、等腰三角形三线合一的性质、三角形的内角和定理等知识,寻找相似三角形是解决问题的关键.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源:2017届江苏省徐州市九年级下学期第一次(3月)月考数学试卷(解析版) 题型:单选题
如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )
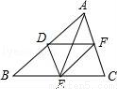
A. AB⊥AC B. AB=AC C. AB=BC D. AC=BC
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司开发了一种新型的家电产品,现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=$\left\{\begin{array}{l}{3x(0≤x≤25)}\\{2x+25(25<x≤40)}\end{array}\right.$,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
某公司开发了一种新型的家电产品,现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=$\left\{\begin{array}{l}{3x(0≤x≤25)}\\{2x+25(25<x≤40)}\end{array}\right.$,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com