
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
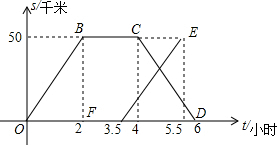 为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进)
为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
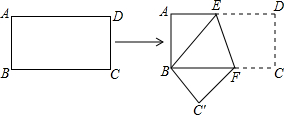
 如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.若CG=8,则S四边形BCDG=16$\sqrt{3}$.
如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.若CG=8,则S四边形BCDG=16$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 6 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com