
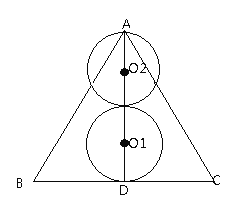
【题目】已知等边△ABC边长为2,D为BC中点,连接AD.点O在线段AD上运动(不含端点A、D),以点O为圆心,![]() 长为半径作圆,当
长为半径作圆,当![]() O与△ABC的边有且只有两个公共点时,DO的取值范围为_____.
O与△ABC的边有且只有两个公共点时,DO的取值范围为_____.
【答案】![]() 或
或![]()
【解析】
根据题意作图,根据![]() O与△ABC的边有且只有两个公共点时得到两种情况,分别讨论求解即可.
O与△ABC的边有且只有两个公共点时得到两种情况,分别讨论求解即可.
∵![]() O与△ABC的边有且只有两个公共点
O与△ABC的边有且只有两个公共点
∴①当圆O与BC相交于两点时,
如图,点圆O1与BC相切时,恰好有一个交点,此时,O1D=![]() ,
,
故当![]() 时,
时,![]() O与△ABC的边有且只有两个公共点;
O与△ABC的边有且只有两个公共点;
②当圆O与△ABC的AB、AC各交于一点时,
∵等边△ABC边长为2,D为BC中点
∴∠B=∠BAC=60°,AD为△ABC的高、中线、∠BAC的角平分线,
∴BD=1,则AD=![]()
如图,圆O2与△交于3点,此时AO2=![]() ,
,
则O2D=![]() -
-![]() =
=![]()
∵![]() O与△ABC的边有且只有两个公共点,则点A在圆O内部,
O与△ABC的边有且只有两个公共点,则点A在圆O内部,
∴当![]() 时,
时,![]() O与△ABC的边有且只有两个公共点;
O与△ABC的边有且只有两个公共点;
综上,当![]() 或
或![]() 时,
时,![]() O与△ABC的边有且只有两个公共点.
O与△ABC的边有且只有两个公共点.
故填:![]() 或
或![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
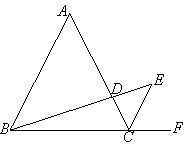
(1)求证:△ABD∽△CED.
(2)若AB=6,AD=2CD,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
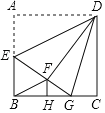
【题目】如图,正方形ABCD中,AB=6,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G,FH⊥BC,垂足为H,连接BF、DG.以下结论:①BF∥ED;②△DFG≌△DCG;③△FHB∽△EAD;④tan∠GEB=![]() ;⑤S△BFG=2.6;其中正确的个数是( )
;⑤S△BFG=2.6;其中正确的个数是( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
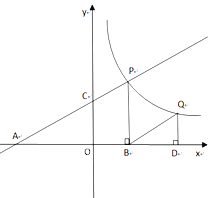
【题目】如图,直线y=![]() x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点Q与点P在同一个反比例函数的图象上,且点Q在直线PB的右侧,作QD⊥x轴于D,当△BQD与△AOC相似时,求点Q的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
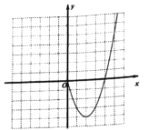
【题目】某课外学习小组根据学习函数的经验,对函数![]() 的图象与性质进行了探究请补充完整以下探索过程:
的图象与性质进行了探究请补充完整以下探索过程:
(1)列表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接写出![]() ________,
________,![]() ________;
________;
(2)根据上表中的数据,在平面直角坐标系内补全该函数的图象,并结合图象写出该函数的两条性质:
性质1______________________________________________________
性质2_______________________________________________________
(3)若方程![]() 有四个不同的实数根,请根据函数图象,直接写出k的取值范围.
有四个不同的实数根,请根据函数图象,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
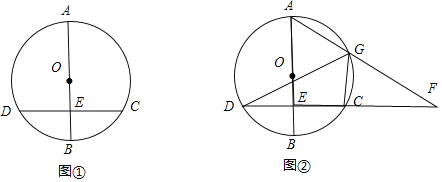
【题目】已知AB是⊙O的直径,弦CD⊥AB于点E.
(1)如图①,若CD=8,BE=2,求⊙O的半径;
(2)如图②,点G是![]() 上一点,AG的延长线与DC的延长线交于点F,求证:∠AGD=∠FGC.
上一点,AG的延长线与DC的延长线交于点F,求证:∠AGD=∠FGC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备进一批季节性小家电,进价为每台40元,经市场预测,售价为每台48元时,可售出220台;售价每增加1元,销售量减少10台。
(1)当售价为55元,销售量为多少台?
(2)因受库存的影响,每批次进货个数不得超过160台,若商店想获得2000元利润,则应进货多少台?售价定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com