
| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
科目:初中数学 来源: 题型:选择题
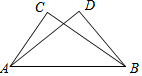 如图,已知∠ACB=∠ADB=90°,AC=BD.又因为公共边AB=BA,所以△ABC≌△BAD,其理由是( )
如图,已知∠ACB=∠ADB=90°,AC=BD.又因为公共边AB=BA,所以△ABC≌△BAD,其理由是( )| A. | SAS | B. | ASA | C. | SSA | D. | HL |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表
将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表| 所剪次数 | 1 | 2 | 3 | 4 | … | n |
| 正三角形个数 | 4 | 7 | 10 | 13 | … | an |
| A. | 2n | B. | 3(n-1) | C. | 3(n+1) | D. | 3n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
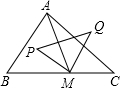 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC,AC的长为8cm,AC边上的高为BD,当B点在线段BD上向D点运动时,△ABC的面积发生了变化.
如图,在△ABC,AC的长为8cm,AC边上的高为BD,当B点在线段BD上向D点运动时,△ABC的面积发生了变化.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>0>y2 | B. | y1>y2>0 | C. | y2>0>y1 | D. | 0>y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3-$2\sqrt{2}$ | B. | 3+$2\sqrt{2}$ | C. | 6-4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com