
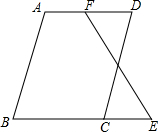
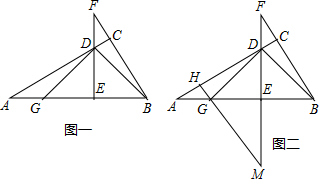
 如图,已知∠B+∠BCD=180°,∠B=∠D,求证:∠E=∠DFE.
如图,已知∠B+∠BCD=180°,∠B=∠D,求证:∠E=∠DFE. 科目:初中数学 来源: 题型:解答题
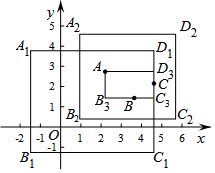 在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
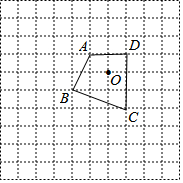 如图,在10×10网格中,四边形ABCD是格点四边形(顶点在网格线的交点上),以点O为位似中心,在网格中把四边形ABCD放大为原来的3倍.
如图,在10×10网格中,四边形ABCD是格点四边形(顶点在网格线的交点上),以点O为位似中心,在网格中把四边形ABCD放大为原来的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系xOy中,?OABC的边OC在x轴上,A(1,4)、C(3,0)点D在AB上,D(3,4),过点D的直线l平分?OABC的面积,现将l绕点A逆时针旋转90°得直线l′,则直线l′的函数解析式为( )
如图,在平面直角坐标系xOy中,?OABC的边OC在x轴上,A(1,4)、C(3,0)点D在AB上,D(3,4),过点D的直线l平分?OABC的面积,现将l绕点A逆时针旋转90°得直线l′,则直线l′的函数解析式为( )| A. | y=-2x+6 | B. | y=-2x+6.5 | C. | $y=-\frac{1}{2}x+\frac{5}{2}$ | D. | $y=-\frac{1}{2}x+\frac{13}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
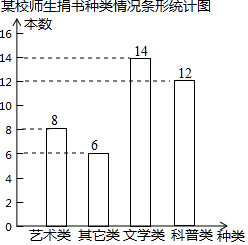 为了解某校师生捐书情况,随机调查了部分师生,根据调查结果绘制了如图所示的统计图.若该校共有师生1000人,则捐文学类书籍的师生约有350人.
为了解某校师生捐书情况,随机调查了部分师生,根据调查结果绘制了如图所示的统计图.若该校共有师生1000人,则捐文学类书籍的师生约有350人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=-2x+2分别与x轴,y轴交于点C,B,并且与某一反比例函数y=$\frac{m}{x}$在第二象限交于点A(-1,a),过点B作直线AC的垂线交x轴于点E,交另一双曲线y=$\frac{n}{x}$于点D(b,-2).
已知直线y=-2x+2分别与x轴,y轴交于点C,B,并且与某一反比例函数y=$\frac{m}{x}$在第二象限交于点A(-1,a),过点B作直线AC的垂线交x轴于点E,交另一双曲线y=$\frac{n}{x}$于点D(b,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com