
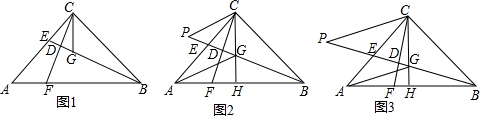
���� ��1������ASA֤����BCG�ա�CAF����CF=BG��
��2����֤����ACG�ա�BCG���á�CAG=��CBE����֤����PCG=��PGC�����ɵó����ۣ�
��3������AEG�ĸ���EM�����ݽǵĴ�С��ϵ�ó���CAG=30�㣬����������EM�ij�������30��ǵ����Ǻ���ֵ������AE��EG��BE�ij�������CE=3+$\sqrt{3}$�������߶εĺ͵ó�AC�ij���
��� ֤������1����ͼ1���ߡ�ACB=90�㣬AC=BC��
���A=45�㣬
��CGƽ�֡�ACB��
���ACG=��BCG=45�㣬
���A=��BCG��
�ڡ�BCG�͡�CAF�У�
��$\left\{\begin{array}{l}{��A=��BCG}\\{AC=BC}\\{��ACF=��CBE}\end{array}\right.$��
���BCG�ա�CAF��ASA����
��CF=BG��
��2����ͼ2����PC��AG��
���PCA=��CAG��
��AC=BC����ACG=��BCG��CG=CG��
���ACG�ա�BCG��
���CAG=��CBE��
�ߡ�PCG=��PCA+��ACG=��CAG+45��=��CBE+45�㣬
��PGC=��GCB+��CBE=��CBE+45�㣬
���PCG=��PGC��
��PC=PG��
��PB=BG+PG��BG=CF��
��PB=CF+CP��
��3����ͼ3����E��EM��AG����AG��M��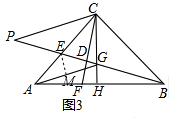
��S��AEG=$\frac{1}{2}$AG•EM=3$\sqrt{3}$��
�ɣ�2���ã���ACG�ա�BCG��
��BG=AG=6��
��$\frac{1}{2}$��6��EM=3$\sqrt{3}$��
EM=$\sqrt{3}$��
���FCH=x�㣬���GAC=2x�㣬
���ACF=��EBC=��GAC=2x�㣬
�ߡ�ACH=45�㣬
��2x+x=45��
x=15��
���ACF=��GAC=30�㣬
��Rt��AEM��AE=2EM=2$\sqrt{3}$��
AM=$\sqrt{��2\sqrt{3}��^{2}-��\sqrt{3}��^{2}}$=3��
��M��AG���е㣬
��AE=EG=2$\sqrt{3}$��
��BE=BG+EG=6+2$\sqrt{3}$��
��Rt��ECB�У���EBC=30�㣬
��CE=$\frac{1}{2}$BE=3+$\sqrt{3}$��
��AC=AE+EC=2$\sqrt{3}$+3+$\sqrt{3}$=3$\sqrt{3}$+3��
���� ���⿼����ȫ�������ε����ʺ��ж�������ֱ�������ε����ʣ�֤�����߶����ʱ��һ�㶼��֤�����߶����ڵ�������ȫ�ȣ���˵�һ��ֻ��Ҫ֤����BCG�ա�CAF���ɣ���3�ʣ���εó�30��Ǻ��������ߣ����õ�S��AEG=3$\sqrt{3}$��ʽ��ͻ�ƿڣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��D��E�ֱ��ǡ�ABC����AB��AC�ϵĵ㣬���������������¡�ADE���ACB�Ƿ����ƣ���˵�����ɣ�
��֪����ͼ��D��E�ֱ��ǡ�ABC����AB��AC�ϵĵ㣬���������������¡�ADE���ACB�Ƿ����ƣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
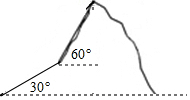 ��ͼ��ij������30���ɽ��ǰ��1000m����ɽ��������Ϊ60�㣬��ǰ��1500m�������ɽ����������ɽ�ĸ߶ȣ�������������
��ͼ��ij������30���ɽ��ǰ��1000m����ɽ��������Ϊ60�㣬��ǰ��1500m�������ɽ����������ɽ�ĸ߶ȣ��������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com