
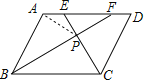
【题目】如图,□ABCD中,BF平分∠ABC交AD于点F,CE平分∠DCB交AD于点E,BF和CE相交于点P.

(1)求证:AE=DF.
(2)已知AB=4,AD=5.
①求![]() 的值;
的值;
②求四边形ABPE的面积与△BPC的面积之比.
【答案】(1)详见解析;(2)①![]() ②
②![]()
【解析】
(1)由平行四边形的性质和角平分线得出∠ABF=∠AFB,得出AF=AB,同理可证DE=DC,推出AF=DE即可解决问题.
(2)①求出EF的值,利用平行线分线段成比例定理即可解决问题.
②连接PA.设△AEP的面积为S.求出四边形ABPE,△PBC的面积即可解决问题.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
则∠ABF=∠AFB,
∴AF=AB,
同理可证:DE=DC,
∴AF=DE,
∴AE=DF.
(2)①解:由(1)可知AB=AF=DE=4,
∴AE=DF=1,EF=3,
∵EF∥BC,
∴![]() .
.
②解:连接PA.设△AEP的面积为S.
∵AE= 1,EF=3,
∵EF=3AE,
∴△EFP的面积为3S,
∵AD∥BC,
∵△EFP∽△CBP,
∴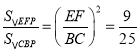 ,
,
∴S△BCP=![]() S,
S,
∵PB:PF=5:3,
∴S△APB:S△APF=5:3,
∴S△ABP=![]() S,
S,
∴S四边形ABPE= S△ABP +S△AEP =![]() S,
S,
∴ .
.


科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,点
边的中点,点![]() 在
在![]() 上,连接
上,连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)如图1,连接![]() ,当
,当![]() 时,求证:
时,求证:![]()
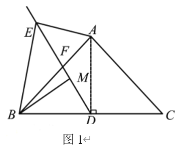
(2)如图2,当![]() 时,则线段
时,则线段![]() 之间的数量关系为 ;
之间的数量关系为 ;
(3)在(2)的条件下,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求证:
,求证:![]() ,并求
,并求![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
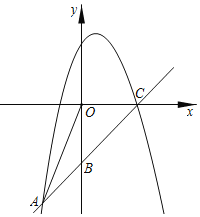
【题目】如图,已知一次函数y=kx+b的图象经过A(﹣1,﹣5),B(0,﹣4)两点且与x轴交于点C,二次函数y=ax2+bx+4的图象经过点A、点C.
(1)求一次函数和二次函数的函数表达式;
(2)连接OA,求∠OAB的正弦值;
(3)若点D在x轴的正半轴上,是否存在以点D,C,B构成的三角形与△OAB相似?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
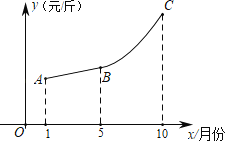
【题目】今年的猪肉价格一直以来一路飙升,市民们一致声称:吃不起!近日,王老师通过相关部门了解到2019年1月到10月湖州各大超市的猪肉的月平均售价,并绘制了如图所示的函数图象,其中1月份到5月份的猪肉售价y与月份x之间的关系符合线段AB,5月份到10月份的猪肉售价y与月份x之间的关系符合抛物线BC.已知点A(1,16),点B(5,17),点C(10,42),且点B是抛物线的顶点.
(1)求线段AB和抛物线BC的解析式;
(2)已知1月份到5月份猪肉的平均进价为13元/斤,5月份到10月份猪肉的平均进价z与月份x之间的关系为z=3x﹣2(x为正整数),若设每销售一斤猪肉获得的利润为w,试求1月到10月w至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对钝角α,定义三角函数值如下:
sinα=sin(180°-α),cosα=-cos(180°-α).
(1)求sin120°,cos120°的值;
(2)若一个钝角三角形的三个内角比是1:1:4,点A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房的成交均价由2019年8月份的8000元/![]() 下降到2019年10月份的7500元/
下降到2019年10月份的7500元/![]() .
.
(1)求2019年9、10两月该市的商品房成交均价平均每月降价的百分率(精确到0.1,参考数据:![]() );
);
(2)如果房价继续回落,按(1)的降价的百分率,你认为到2019年12月份该市的商品房成交均价会跌破7000元/![]() 吗?请说明理由.
吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
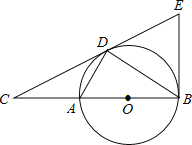
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
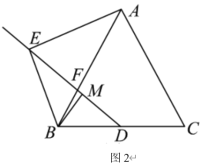
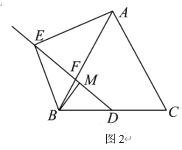
【题目】△ABC和△CDE是以点C为公共顶点的两个三角形.
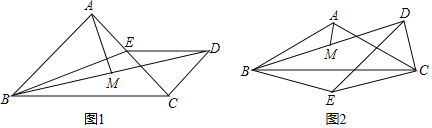
(1)如图1,当AB=AC,CD=CE,∠BAC=∠DCE=90°时,连接BD,取BD的中点M,连接AM.探究AM、BE之间的数量关系,并证明你的结论;
(2)如图2,当AB=AC,∠BAC=120°,∠CDE=60°,∠DCE=90°时,连接BD,取BD的中点M,连接AM.探究AM、BE之间的关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com