
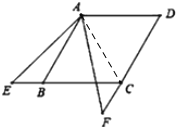
【题目】如图所示,菱形ABCD中,AB=5,∠ABC=60°,∠EAF=60°,∠EAF的两边分别交BC、CD于E、F.
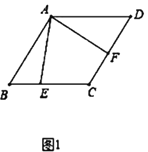
(1)如图1所示,当点E、F分别在边BC、CD上时,求CE+CF的值;
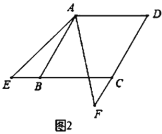
(2)如图2所示,当点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 的延长线时,请从
的延长线时,请从![]() ,
,![]() 两题中任选一题作答,我选______题.
两题中任选一题作答,我选______题.
![]() 题:则
题:则![]() 的值是________.
的值是________.
![]() 题:则
题:则![]() 与
与![]() 的关系是________.
的关系是________.
【答案】(1)CE+CF=5;(2)A题:5;B题:CE-CF=5.
【解析】
(1)如图,连接AC,由菱形的性质可得AB=AD=BC=CD,∠D=∠ABC=60°,可得△ABC和△ADC都是等边三角形,即可证明AC=AD,∠CAD=60°,根据角的和差关系可得∠EAC=∠FAD,利用ASA可证明△EAC≌△FAD,可得CE=DF,即可得出CF+CE=CF+DF=CD,可得答案;
(2)A题:如图,连接AC,由角的和差关系可得∠EAB=∠FAC,利用平角定义可得∠ABE=∠ACF,利用ASA可证明△AEB≌△AFC,可得BE=CF,即可得出CE-CF=CE-BE=BC,可得答案;
B题:同A题解法可得答案.
(1)如图,连接AC,
∵四边形ABCD是菱形,∠ABC=60°,
∴AB=AD=BC=CD,∠D=∠ABC=60°,
∴△ABC和△ADC都是等边三角形,
∴AC=AD,∠CAD=∠ACE=∠D=60°,
∵EAF=60°,
∴∠EAC+∠FAC=∠FAD+∠FAC=60°,
∴∠EAC=∠FAD,
在△EAC和△FAD中,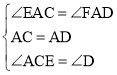 ,
,
∴△EAC≌△FAD,
∴CE=DF,
∵AB=5,
∴CE+CF=CF+DF=CD=AB=5,
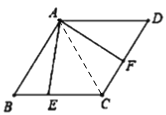
(2)A题:如图,连接AC,
∵∠BAC=∠EAF=60°,
∴∠EAB+∠BAF=∠CAF+∠BAF,
∴∠EAB=∠CAF,
∵∠ABC=∠ACD=60°,
∴∠ABE=∠ACF=120°,
在△ABE和△ACF中,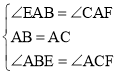 ,
,
∴△ABE≌△ACF,
∴BE=CF,
∴CE-CF=CE-BE=BC=5.
故答案为:5
B题:同A题解法可得CE-CF=5.
故答案为:CE-CF=5


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
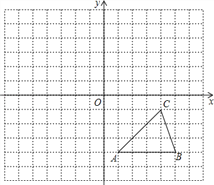
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
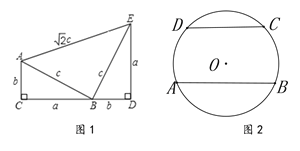
【题目】如图1,四边形ACDE是美国第二十任总统伽菲尔德验证勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE=![]() ,这时我们把关于x的形如
,这时我们把关于x的形如![]() 的一元二次方程称为“勾系一元二次方程”.
的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)判断方程![]() 是否是 “勾系一元二次方程”;并说明理由.
是否是 “勾系一元二次方程”;并说明理由.
(2)求证:关于![]() 的“勾系一元二次方程”
的“勾系一元二次方程” ![]() 必有实数根;
必有实数根;
(3)如图2,已知AB、CD是半径为5的⊙O的两条平行弦,AB=2a,CD=2b,a≠b,关于x的方程![]() 是“勾系一元二次方程”,求∠BAC的度数
是“勾系一元二次方程”,求∠BAC的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店店主对书店销售情况进行统计,店主根据一个月内平均每天各销售时间段内的销售量,绘制了如下尚不完整的统计图表.
销售情况扇形统计图
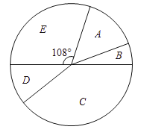
销售情况统计表
销售时间段 | 销售数量(本) |
| 16 |
|
|
| 37 |
| 12 |
| 30 |
合计 |
|
根据以上信息,回答下列问题:
(1)平均每天的销售总量![]() ________,
________,![]() 时间段每天的销售数量
时间段每天的销售数量![]() ___________.
___________.
(2)求出![]() 时间段所在扇形的圆心角的度数.
时间段所在扇形的圆心角的度数.
(3)若该书店一年的销量有32000本,请你估计![]() 时间段全年卖出多少本.
时间段全年卖出多少本.
(4)若书店决定减少成本,同时保证销量,决定在某时间段闭店,请你提出一条合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
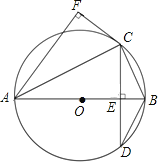
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
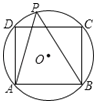
A.45° B.60° C.45° 或135° D.60° 或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com