练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．如图，在△ABC中，∠BAC=90°，AC=2，AB=4，将△ABC折叠，使点B和点C重合，折痕为DE，则AE的长为2．

    分析 由折叠可知：EC=BE，设AE=x，则EC=BE=4-x，在直角△ACE中，利用勾股定理建立方程求得答案即可．

    解答 解：∵将△ABC折叠，使点B和点C重合，折痕为DE，
    ∴EC=BE，
    设AE=x，则EC=BE=4-x，
    在直角△ACE中，
    AE2+AC2=CE2，
    即x2+22=（4-x）2，
    解得：x=2．
    即AE=2．
    故答案为：2．

    点评 此题考查图形的翻折变化，勾股定理的运用，结合图形，把已知条件和所求问题转化在一个三角形内是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．在下列实数中，无理数是（　　）
    A．3.14B．1C．$\frac{1}{3}$D．$\sqrt{6}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，AB∥CD，直线EF分别交AB、CD于点E、F，HF平分∠EFD，若∠1=110°，则∠2的度数为（　　）
    A．55°B．40°C．35°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

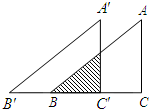    11．如图，△ABC≌△A′B′C′，∠C=∠C′=90°，AC=3cm，A′B′=5cm，先将△ABC和△A′B′C′完全重合，再将△ABC固定，△A′B′C′沿CB所在的直线向左以每秒1cm的速度平行移动，3秒后重叠部分的面积为$\frac{3}{8}$cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

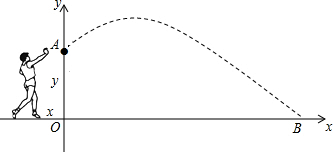    18．校运会上，小明参加铅球比赛，若某次试掷，铅球飞行的高度y（m）与水平距离x（m）之间的函数关系式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$，求：
    （1）铅球的出手时的高度；
    （2）小明这次试掷的成绩．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向下、向右的方向一次不断移动，每次移动1个单位，其行走路线如图所示．

    （1）填写下列各点的坐标：A1（0，1），A2（1，1）；
    （2）写出点A4n的坐标（n是正整数）；
    （3）指出蚂蚁从点A100到点A101的移动方向．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．已知点A（1，2），O是坐标原点，将线段OA绕点O逆时针旋转90°，点A旋转后的对应点是A1，则点A1的坐标是（　　）
    A．（-2，1）B．（2，-1）C．（-1，2）D．（-1，-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

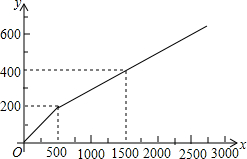    12．为加强与家长的沟通，某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传，该校的印刷任务原来由甲复印店承接，其收费y（元）与印刷页数x（页）的函数关系如图所示．
    （1）从图象中可看出：印刷超过500页部分每页收费0.2元；
    （2）现在乙印刷厂表示：每页0.15元收费．另收200元的制版费，乙印刷厂收费y（元）与印刷页数x（页）的函数关系为y=0.15x+200（x≥0）；
    （3）在给出的坐标系内画出（2）中的函数图象，并结合函数图象回答印刷页数在3000页左右应选择哪个印刷店？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，已知等腰直角三角形ABC的直角边长与正方形DEFG的边长都是4cm，AC与DG在同一直线上，开始时点A与点D重合，△ABC以1cm/s的速度向右移动，最终点A与点G重合，设重合部分（阴影部分）的面积为y（cm2），移动的时间为x（s）．
    （1）求出y与x的函数关系式；
    （2）画出（1）中所写出的函数关系式的图象．
    ①完成下表：
     x/s     
     y/cm2     
    ②画出图象．

    查看答案和解析>>

    同步练习册答案