
分析 (1)利用“k类生长点”的定义求解;
(2)先得到点P的“1类生长点”为P′点坐标为(a+b,a+b),则可判断点P′在第一象限的角平分线上,再利用菱形的性质可判断点P与点A关于OP′对称,所以P(4,3),则P′(7,7),然后利用勾股定理计算出
∴AP和OP′,再利用菱形的面积公式求解.
解答 解:(1)点P(1,4)的“2类生长点”P′的坐标为(1+2×4,2×1+4),即P′(9,6);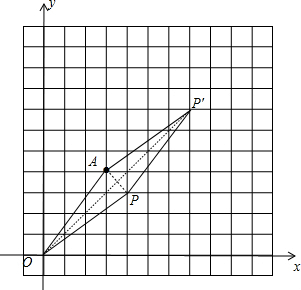
故答案为(9,6);
(2)∵点P的“1类生长点”为P′点坐标为(a+b,a+b),
∴点P′在第一象限的角平分线上,
∵四边形OPP′A是菱形,
∴点P与点A关于OP′对称,
∴P(4,3),
∴P′(7,7),
∴AP=$\sqrt{2}$,OP′=7$\sqrt{2}$,
∴该菱形的面积=$\frac{1}{2}$×$\sqrt{2}$×7$\sqrt{2}$=7.
点评 本题考查了菱形的性质:有一组邻边相等的平行四边形叫做菱形.熟练掌握菱形的性质(菱形具有平行四边形的一切性质; 菱形的四条边都相等; 菱形的两条对角线互相垂直,并且每一条对角线平分一组对角). 解决(1)小题的关键是理解“k类生长点”的定义.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=2,则AB的长是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=2,则AB的长是( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 4$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10% | B. | 15% | C. | 20% | D. | 25% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点M,N分别在∠AOB的边OA,OB上,且OM=ON.
如图,点M,N分别在∠AOB的边OA,OB上,且OM=ON.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com