
【题目】如图,在平面直角坐标系中,点A的坐标为(2![]() ,2
,2![]() ),点P在直线y=﹣x上运动,∠PAB=90°,∠APB=30°,在点P运动的过程中OB的最小值为( )
),点P在直线y=﹣x上运动,∠PAB=90°,∠APB=30°,在点P运动的过程中OB的最小值为( )
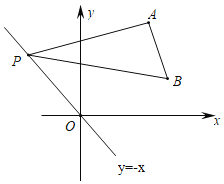
A.3.5B.2C.![]() D.2
D.2![]()
【答案】D
【解析】
如图中,作BH⊥OP于H,取PB的中点F,连接AF、FH、OA、AH.首先证明点B在射线HB上运动,推出当OB⊥BH时,OB的值最小,最小值为OH的长;
解:如图,作BH⊥OP于H,取PB的中点F,连接AF、FH、OA、AH.

在Rt△PAB和Rt△PBH中,
∵PF=FB,
∴AF=PF=FB=FH,
∴A、P、H、B四点共圆,
∵∠PAB=90°,∠APB=30°
∴![]()
∴∠AHB=∠APB=30°,∠AHP=∠ABP =60°,
∴点B在射线HB上运动,
∴当OB⊥BH时,OB的值最小,最小值为OH的长,
在Rt△AOH中,A(2![]() ,2
,2![]() )
)
∴OA=2![]() ,∠AHO=60°,
,∠AHO=60°,
∴OH=2![]() ,
,
∴OB的最小值为2![]() .
.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x+2与x轴、y轴分别交于点B,C,抛物线y=
x+2与x轴、y轴分别交于点B,C,抛物线y=![]() x2+bx+c过点B、C,且与x轴交于另一个点A.
x2+bx+c过点B、C,且与x轴交于另一个点A.
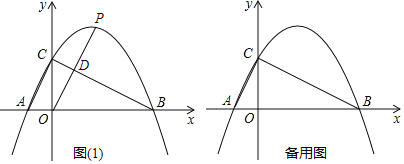
(1)求该抛物线的表达式;
(2)若点P是x轴上方抛物线上一点,连接OP.
①若OP与线段BC交于点D,则当D为OP中点时,求出点P坐标.
②在抛物线上是否存在点P,使得∠POC=∠ACO若存在,求出点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东45°方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上.
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东30°的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
(参考数据:sin22°≈0.375,cos22°≈0.927,tan22°≈0.404,![]() ≈1.732.)
≈1.732.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日
日![]() 商用套餐正式上线.某移动营业厅为了吸引用户,设计了
商用套餐正式上线.某移动营业厅为了吸引用户,设计了![]() ,
,![]() 两个可以自由转动的转盘(如图),
两个可以自由转动的转盘(如图),![]() 转盘被等分为
转盘被等分为![]() 个扇形,分别为红色和黄色;
个扇形,分别为红色和黄色;![]() 转盘被等分为
转盘被等分为![]() 个扇形,分别为黄色、红色、蓝色,指针固定不动.营业厅规定,每位
个扇形,分别为黄色、红色、蓝色,指针固定不动.营业厅规定,每位![]() 新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取
新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取![]() 通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形).小王办理
通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形).小王办理![]() 业务获得一次转转盘的机会,求他能免费领取
业务获得一次转转盘的机会,求他能免费领取![]() 通用流量的概率.
通用流量的概率.

A B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光污染是继废气、废水、废渣和噪声等污染之后的一种新的环境污染源,主要包括白亮污染、人工白昼污染和彩光污染,如图,小明家正对面的高楼外墙上安装着一幅巨型广告宣传牌AB,小明想要测量窗外的广告宣传牌AB的高度,他发现晚上家里熄灯后对面楼上的广告宣传牌从A处发出的光恰好从窗户的最高点C处射进房间落在地板上F处,从窗户的最低点D处射进房间向落在地板上E处(B、O、E、F在同一直线E),小明测得窗户距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=3m.请根据以上测量数据,求广告宣传牌AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像经过点
的图像经过点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
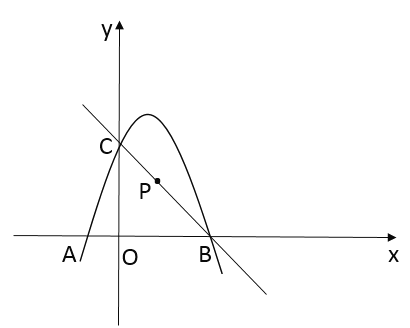
(1)求![]() 、
、![]() 的值:
的值:
(2)若点![]() 为直线
为直线![]() 上一点,点
上一点,点![]() 到直线
到直线![]() 、
、![]() 两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点
两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点![]() ,求新抛物线的顶点坐标.
,求新抛物线的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个函数y1和y2的自变量x的取值范围相同,我们不妨把y1和y2的比值y称为x的比函数,且比函数的自变量x的取值范围不发生改变.例如:y1=x2+2x(x>0),y2=x(x>0),则x的比函数为y=![]() =x+2(x>0).
=x+2(x>0).
(1)已知y1=x2﹣4(2≤x≤3),y2=x+2(2≤x≤3),写出x的比函数y的解析式,并求出y的取值范围;
(2)已知y1=x+2(x>1),y2=x﹣2(x>1),求x的比函数y的图象上的整数点(横坐标和纵坐标都为整数的点)的坐标;
(3)已知y1=x2﹣x+1,y2=x2+x+1,若x的比函数y的图象与抛物线y3=x2+2x+k(k为常数)存在交点,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com