
【题目】如图![]() ,在
,在![]() 中,
中,![]() 、
、![]() 的平分线相交于点O
的平分线相交于点O
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 若
若![]() ,则
,则![]() ______ ;
______ ;
![]() 若
若![]() ,则
,则![]() ______ ;
______ ;
![]() 如图
如图![]() ,在
,在![]() 中的外角平分线相交于点
中的外角平分线相交于点![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 上面
上面![]() ,
,![]() 两题中的
两题中的![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?

【答案】(1)(a)120°; (b) 90°+![]() n°;(c)36°; (2)36°;(3) ∠B′O′C′=180°-∠BOC.
n°;(c)36°; (2)36°;(3) ∠B′O′C′=180°-∠BOC.
【解析】
(1)(2)根据三角形内角和定理和角平分线定义解答;(3)由前两问提供的思路,进一步推理.
(1)(a)∵∠ABC、∠ACB的平分线相交于点O,
∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB,
∠ACB,
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=
(180°-∠A)=![]() ×(180°-60°)=60°,
×(180°-60°)=60°,
∴∠BOC=180°-60°=120°;
(b)方法同(a)可得:90°+![]() n°;
n°;
(c) 由(a)、(b)结论知:∠BOC= 90°+![]() ∠A,又因为
∠A,又因为![]() ,
,
∴ 90°+![]() ∠A=3∠A,解得:∠A= 36°;
∠A=3∠A,解得:∠A= 36°;
(2)∵∠A'=40°,
∴∠A'的外角等于180°-40°=140°,
∵△A′B′C′另外的两外角平分线相交于点O′,三角形的外角和等于360°,
∴∠1+∠2=![]() ×(360°-140°)=110°,
×(360°-140°)=110°,
∴∠B′O′C′=180°-110°=70°;
(3)∵由(1)知,∠BOC=![]() ,由(2)知,∠B′O′C′=180°-
,由(2)知,∠B′O′C′=180°-![]() ,
,
∴∠B′O′C′=180°-∠BOC.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某产品的进价为![]() 元,该产品的日销量
元,该产品的日销量![]() (件)是日销价
(件)是日销价![]() (元)的反比例函数,且当售价为每件
(元)的反比例函数,且当售价为每件![]() 元时,每日可售出
元时,每日可售出![]() 件,为获得日利润为
件,为获得日利润为![]() 元,售价应定为________.
元,售价应定为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() .
.
![]() 求证:抛物线总与
求证:抛物线总与![]() 轴有两个不同的交点;
轴有两个不同的交点;
![]() 若
若![]() ,求此抛物线的解析式.
,求此抛物线的解析式.
![]() 已知
已知![]() 轴上两点
轴上两点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有交点,请写出
有交点,请写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价
元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件,若商场平均每天要盈利
件,若商场平均每天要盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设门市部专卖某产品,该产品每件成本![]() 元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
每件销售价(元) |
|
|
|
|
|
| … |
每天售出件数 |
|
|
|
|
|
| … |
假设当天定的售价是不变的,且每天销售情况均服从这种规律.
![]() 观察这些统计数据,找出每天售出件数
观察这些统计数据,找出每天售出件数![]() 与每件售价
与每件售价![]() (元)之间的函数关系,并写出该函数关系式.
(元)之间的函数关系,并写出该函数关系式.
![]() 门市部原设有两名营业员,但当销售量较大时,在每天售出量超过
门市部原设有两名营业员,但当销售量较大时,在每天售出量超过![]() 件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为
件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为![]() 元.求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)
元.求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ABC=90°,AB=BC,点A,B分别在坐标轴上.
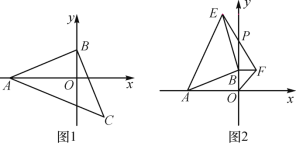
(1)如图1,若点C的横坐标为5,直接写出点B的坐标 ;
(2)如图2,若点A的坐标为(-6,0),点B在y轴的正半轴上运动时,分别以OB,AB为边在第一、第二象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,直线AB交
中,直线AB交![]() 轴于A(2,0),交
轴于A(2,0),交![]() 轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
(1)求△ABC的面积.
(2)延长BA到P(自己补全图形),使得PA=AB,过点P作PM⊥OC于M,求P点的坐标.
(3)如图,D是第三象限内一动点,直线BE⊥CD于E, OF⊥OD交BE延长线于F.当D点运动时,![]() 的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.
的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒1 cm的速度沿折线
出发,以每秒1 cm的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒(
秒(![]() >0).
>0).

(1)若点![]() 在
在![]() 上,且满足
上,且满足![]() ,求此时
,求此时![]() 的值;
的值;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值;
的值;
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com