
| A.① | B.①② | C.② | D.③④ |
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:新课标读想练同步测试 八年级数学(下) 人教版 题型:044
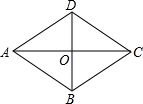
如图所示,某村有一片呈四边形的池塘,在它的四个角A、B、C、D处均种有一棵大树,村民准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持大树不动.并要求扩建后的池塘成平行四边形状,请问该村能否实现这一设想?若能,请你设计并画出图形;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2007年广西省河池市中等学校招生统一考试试题卷数学(非课改区) 题型:059
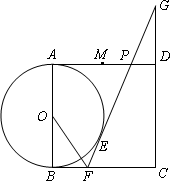
如图,已知正方形ABCD的边长为![]() ,点M是AD的中点,P是线段MD上的一动点(P不与M,D重合),以AB为直径作⊙O,过点P作⊙O的切线交BC于点F,切点为E.
,点M是AD的中点,P是线段MD上的一动点(P不与M,D重合),以AB为直径作⊙O,过点P作⊙O的切线交BC于点F,切点为E.

(1)除正方形ABCD的四边和⊙O中的半径外,图中还有哪些相等的线段(不能添加字母和辅助线)?
(2)求四边形CDPF的周长;
(3)延长CD,FP相交于点G,如图所示.是否存在点P,使BF·FG=CF·OF?如果存在,试求此时AP的长;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com