
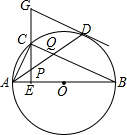
 如图,在⊙O中.AB是直径,点D是⊙O上-点.点C是$\widehat{AD}$的中点,CE⊥AB于点E,在EC的延长线上有一点G,使GP=GD.连接AD,分别交CE、CB于点P、Q,连接AC,且AC=6,BC=8.
如图,在⊙O中.AB是直径,点D是⊙O上-点.点C是$\widehat{AD}$的中点,CE⊥AB于点E,在EC的延长线上有一点G,使GP=GD.连接AD,分别交CE、CB于点P、Q,连接AC,且AC=6,BC=8.分析 (1)连接OD,利用等腰三角形的性质,可得出∠GPD=∠GDP,∠OAD=∠ODA,进一步证得∠APF+∠OAD=∠GDP+∠ODA=90°,即OD⊥GD,即可证得GD是⊙O的切线;
(2)证得△ACQ∽△BCA,根据相似三角形的性质即可求得.
解答 解:(1)连接OD,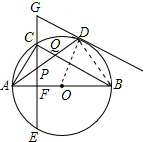
∵GP=GD,
∴∠GPD=∠GDP,
∴∠APF=∠GDP,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠APF+∠OAD=∠GDP+∠ODA,
∵CE⊥AB于点E,
∴∠APF+∠OAD=90°,
∴∠GDP+∠ODA=90°,
即∠ODG=90°,
∴OD⊥GD,
∴GD是⊙O的切线;
(2)∵C点C是$\widehat{AD}$的中点,
∴$\widehat{AC}$=$\widehat{CD}$,
∴∠ABC=∠DBC,
∵∠CAD=∠DBC,
∴∠CAD=∠ABC,
∵∠ACQ=∠BCA,
∴△ACQ∽△BCA,
∴$\frac{AQ}{AB}$=$\frac{AC}{BC}$,
∵AB为圆O的直径,
∴∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴$\frac{AQ}{10}$=$\frac{6}{8}$,
∴AQ=$\frac{15}{2}$.
点评 本题考查了切线的判定,圆周角定理,相似三角形的判定与性质,熟练掌握性质及定理是解决本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
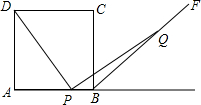 如图,正方形ABCD中,P为边AB上一动点,BF是∠ABC的外角平分线,Q是BF上一点,且PQ=DP,那么DP与PQ是否一定满足垂直关系?说明理由.
如图,正方形ABCD中,P为边AB上一动点,BF是∠ABC的外角平分线,Q是BF上一点,且PQ=DP,那么DP与PQ是否一定满足垂直关系?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩(分) | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 | 91 | 92 | 94 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 | 3 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年份 品种 | 2014年 | 2015年 |
| 平均每亩产量(kg) | 300 | 300(1+x) |
| 养殖面积(亩) | 20 | 20(1+2x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com