
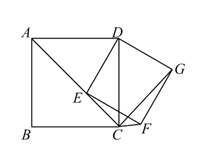
【题目】如图,已知四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG。
(1)求证:矩形DEFG是正方形。
(2)当点E从A点运动到C点时;
①求证:∠DCG的大小始终不变;
②若正方形ABCD的边长为2,则点G运动的路径长为 。
【答案】(1)详见解析;(2)①详见解析;②![]()
【解析】
(1)要证明矩形DEFG为正方形,只需要证明它有一组临边(DE和EF)相等即可,而要证明两条线段相等,需证明它们所在的三角形全等,如下图本小题的关键是证明△EMF≌△END,∠MEF=∠NED可用等角的余角证明,EM=EN可用角平分线上的点到角两边距离相等,∠EMF和∠END为一组直角相等,所以可以用ASA证明它们全等;
(2)此类题,前面的问题是给后面做铺垫,第一问已经证明四边形DEFG为正方形,结合第一问我们很容易发现并证明△ADE≌△CDG,从而得到∠DCG=∠CAD=45°;
(3)当当E点在A处时,点G在C处;当E点在C处时,点G在AD的延长线上,并且AD=DG,以CD为边作正方形,我们会发现G点的运动轨迹刚好是正方形的对角线,它的长度等于![]() .
.
证明:(1)
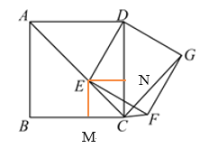
作EM⊥BC,EN⊥CD,
∵四边形ABCD为正方形
∴∠DCB=90°,∠ACB=∠ACD=45°
又∵EM⊥BC,EN⊥CD,
∴EM=EN(角平分线上的点到角两边距离相等),
∠MEN=90°,
∴∠MEF+∠NEF=90°,
∵四边形DEFG为矩形,
∴∠DEF=90°,
∴∠NED+∠NEF=90°,
∴∠MEF=∠NED,
在△EMF和△END中
∵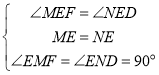
∴△EMF≌△END,
∴DE=DF,
∴矩形DEFG为正方形;
(2)①证明:∵正方形ABCD、DEFG
∴AD=CD,ED=GD
∵∠ADE+∠DEC=90°,∠CDG+∠EDC=90°
∴∠ADE=∠CDG
在△ADE和△CDG中,
∵AD=CD,∠ADE=∠CDG,ED=GD
∴△ADE≌△CDG
∴∠DCG=∠EAD=45°
∴∠DCG的大小始终保持不变
②
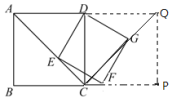
以CD为边作正方形DCPQ,连接QC
∴∠DCQ=45°,
又∵∠DCG=45°
∴C、G、Q在同一条直线上,
当E点在A处时,点G在C处;当E点在C处时,点G在Q处,
∴G点的运动轨迹为QC,
∵正方形ABCD的边长为2
所以QC=![]() ,
,
即点G运动的路径长为![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
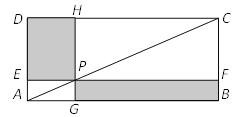
【题目】如图所示,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和点G,H.
(1)求证:△PHC≌△CFP;
(2)证明四边形 PEDH和四边形 PGBF都是矩形,并直接写出它们面积之间的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与发现
(1)正方形ABCD中有菱形PEFG,当它们的对角线重合,且点P与点B重合时(如图1),通过观察或测量,猜想线段AE与CG的数量关系,并证明你的猜想;
(2)当(1)中的菱形PEFG沿着正方形ABCD的对角线平移到如图2的位置时,猜想线段AE与CG的数量关系,只写出猜想不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2019按照一定规律排成下表:
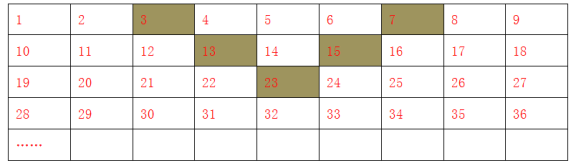
记aij表示第i行第j个数,如a14=4表示第1行第4个数是4.
(1)直接写出a35= ,a54= ;
(2)①若aij=2019,那么i= ,j= ,②用i,j表示aij= ;
(3)将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2026.若能, 求出这5个数中的最小数,若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当![]() = 时,四边形EGFH为矩形。
= 时,四边形EGFH为矩形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图甲是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
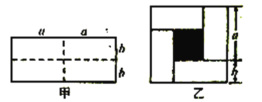
(1)求图乙中阴影部分正方形的边长(用含字母![]() ,
,![]() 的整式表示);
的整式表示);
(2)请用两种不同的方法求图乙中阴影部分的面积.
(3)观察图乙,并结合(2)中的结论,写出下列三个整式:![]() ,
,![]() ,
,![]() 之间的等量关系;
之间的等量关系;
(4)根据(3)题中的等量关系,解决如下问题:若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1955年,印度数学家卡普耶卡(![]() )研究了对四位自然数的一种变换:任给出四位数
)研究了对四位自然数的一种变换:任给出四位数![]() ,用
,用![]() 的四个数字由大到小重新排列成一个四位数
的四个数字由大到小重新排列成一个四位数![]() ,再减去它的反序数
,再减去它的反序数![]() (即将
(即将![]() 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数![]() ,然后继续对
,然后继续对![]() 重复上述变换,得数
重复上述变换,得数![]() ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论![]() 是多大的四位数,只要四个数字不全相同,最多进行
是多大的四位数,只要四个数字不全相同,最多进行![]() 次上述变换,就会出现变换前后相同的四位数
次上述变换,就会出现变换前后相同的四位数![]() ,这个数称为
,这个数称为![]() 变换的核.则四位数9631的
变换的核.则四位数9631的![]() 变换的核为______.
变换的核为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
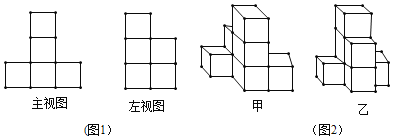
【题目】画图,探究:
(1)一个正方体组合图形的主视图、左视图(如图1)所示.
①这个几何体可能是(图2)甲、乙中的 ;
②这个几何体最多可由 个小正方体构成,请在图3中画出符合最多情况的一个俯视图.
(2)如图,已知一平面内的四个点A、B、C、D,根据要求用直尺画图.
①画线段AB,射线AD;
②找一点M,使M点即在射线AD上,又在直线BC上;
③找一点N,使N到A、B、C、D四个点的距离和最短.
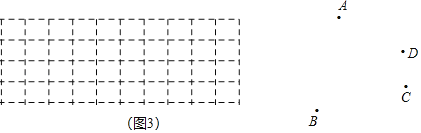
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面中,两条直线相交有一个交点,三条直线两两相交最多有3个交点,四条直线两两相交最多有6个交点……由此猜想,当相交直线的条数为n时,最多可有的交点数m与直线条数n之间的关系式为:m=_____.(用含n的代数式填空)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com