
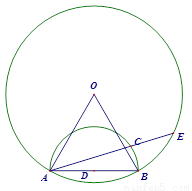
如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以D为圆心似长为半径作
圆O、C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b,
(1)求证:AE=b+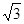 a;
a;
(2)求a+b的最大值;
(3)若m是关于x的方程:x+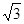 ax=b+
ax=b+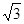 ab的一个根,求m的取值范围.
ab的一个根,求m的取值范围.
(1)连接BE,根据等边三角形的性质可得∠AOB=60°,即得∠AEB=30°,再根据圆周角定理可得∠ACB=∠BCE=90°,根据含30°角的直角三角形的性质可得BE=2a,CE= a,即可得到结果;(2)
a,即可得到结果;(2) 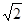 ;(3)
;(3) 或
或
【解析】
试题分析:(1)连接BE,根据等边三角形的性质可得∠AOB=60°,即得∠AEB=30°,再根据圆周角定理可得∠ACB=∠BCE=90°,根据含30°角的直角三角形的性质可得BE=2a,CE= a,即可得到结果;
a,即可得到结果;
(2)过点C作CH⊥AB于H,根据(a+b)2=a2+b2+2ab=1+2ab=1+2CH·AB=1+2CH≤1+2AD=2即可得到结果;
(3)由x+ ax=b+
ax=b+ ab可求得x=b或x=-(b+
ab可求得x=b或x=-(b+ a),分a=m=b与m=-(b+
a),分a=m=b与m=-(b+ a)两种情况分析即可.
a)两种情况分析即可.
(1)连接BE

∵△ABC为等边三角形
∴∠AOB=60°
∴∠AEB=30°
∵AB为直径
∴∠ACB=∠BCE=90°
∵BC=a
∴BE=2a
CE= a
a
∵AC=b
∴AE=b+ a;
a;
(2)过点C作CH⊥AB于H

在Rt△ABC中,BC=a,AC=b,AB=1
∴a2+b2=1
∴(a+b)2=a2+b2+2ab=1+2ab=1+2CH·AB=1+2CH≤1+2AD=2
∴a+b≤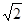 ,故a+b的最大值为
,故a+b的最大值为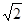 ;
;
(3)x+ ax=b+
ax=b+ ab
ab
∴x-b+ ax-
ax- ab=0
ab=0
(x+b)(x-b)+  a(x-b)=0
a(x-b)=0
(x-b)(x+b+ a)=0
a)=0
∴x=b或x=-(b+ a)
a)
当a=m=b时,m=b=AC<AB=1
∴0<m<1
当m=-(b+ a)时,由(1)知AE=-m
a)时,由(1)知AE=-m
又AB<AE≤2AO=2
∴1<-m≤2
∴-2≤m<-1
∴m的取值范围为 或
或 .
.
考点:圆的综合题
点评:本题知识点较多,综合性强,难度较大,一般是中考压轴题,需要特别注意.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
 如图,在边长为1的等边三角形ABC中,若将两条含120°圆心角的
如图,在边长为1的等边三角形ABC中,若将两条含120°圆心角的 |
| AOB |
 |
| BOC |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )
如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )A、
| ||||
B、
| ||||
C、5
| ||||
D、10
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 交AD于点E,交线段CD于点G,设BP=x.
交AD于点E,交线段CD于点G,设BP=x.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.
(2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.| 3 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com