练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知关于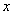的函数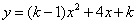的图像与坐标轴只有2个交点，求的值.


    解：分情况讨论：

    （ⅰ）时，得.

    此时与坐标轴有两个交点，符合题意. ……………………………1分

    （ⅱ）时，得到一个二次函数.

    ①     抛物线与x轴只有一个交点，…………………1分

    解得…………………………………………………………2分

         ② 抛物线与x轴有两个交点，其中一个交点是（0,0）…………………1分

            把（0,0）带入函数解析式，易得………………………………1分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


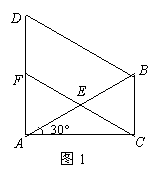
    图1,在△ABC中，∠ACB=90°，∠CAB=30°, △ABD是等边三角形，E是AB的中点，连结CE并延长交AD于F.

    （1）求证：① △AEF≌△BEC；② 四边形BCFD是平行四边形；

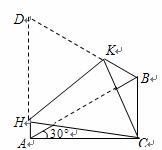
    （2）如图2，将四边形ACBD折叠,使D与C重合，HK为折痕，求sin∠ACH的值.

                                 

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将边长为的等边△ABC折叠，折痕为DE，点B与点F重合，EF和DF分别交于点M、N，DFAB，垂足为D，AD＝1，则重叠部分的面积为          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    函数中自变量x的取值范围是（   ）

    A．x≤3            B．x＝4            C． x＜3且x≠4     D．x≤3且x≠4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某公司有型产品40件，型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完．两商店销售这两种产品每件的利润（元）如下表：

    型利润

    型利润

    甲店

    200

    170

    乙店

    160

    150

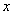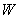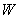    （1）设分配给甲店型产品件，这家公司卖出这100件产品的总利润为（元），求关于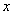的函数关系式，并求出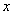的取值范围；

    （2）若公司要求总利润不低于17560元，说明有多少种不同分配方案，并将各种方案设计出来；

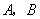    （3）为了促销，公司决定仅对甲店型产品让利销售，每件让利元，但让利后型产品的每件利润仍高于甲店型产品的每件利润．甲店的型产品以及乙店的型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将某图中的横坐标都减去2，纵坐标不变，则该图形（    ）

    A. 向上平移2个单位      B. 向下平移2个单位          

    C. 向右平移2个单位      D. 向左平移2个单位

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，分别延长△ABC的边AB、AC到D、E，∠CBD与∠BCE的平分线相交于点P，爱动脑筋的小明在写作业的时发现如下规律：

    (1)若∠A＝50°，则∠P＝          °；

    (2)若∠A＝90°，则∠P＝          °；

    (3)若∠A＝100°，则∠P＝         °；

    (4)请你用数学表达式归纳∠A与∠P的关系，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点D、E在△ABC的边BC上，AD=AE，AB=AC，求证：BD=EC。（7分）

    查看答案和解析>>

    同步练习册答案