
【题目】如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC.
(1)∠D和∠ECB相等吗?若相等,请说明理由;
(2)△ADC≌△BCE吗?若全等,请说明理由;
(3)能否找到与AB+AD相等的线段,并说明理由。

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】已知在等腰△ABC 中,AB=AC=10,BC=16.
(1)若将△ABC 的腰不变,底变为 12,甲同学说,这两个等腰三角形面积相等;乙同学说,腰不变,底变化,这两个三角形面积必不相等,请对甲、乙两种说法做出判断,并说明理由;
(2)已知△ABC 底边上高增加 x,腰长增加(x﹣2)时,底却保持不变,请确定 x 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师在公园道一号购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:

(1)用含x的代数式表示地面总面积
(2)当x=3时,若铺1m2地砖的平均费用为100元, 那么王老师要将全部地面铺地砖,总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
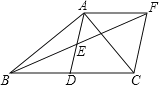
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1) 求证:AD=AF;
(2) 当△ABC满足什么条件时,四边形ADCF是矩形.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2 , 以AD2为一边,做第二个菱形AB2C2D2 , 使∠B2=60°;作AD3⊥B2C2于点D3 , 以AD3为一边做第三个菱形AB3C3D3 , 使∠B3=60°…依此类推,这样做的第n个菱形ABnCnDn的边ADn的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与半径为2的⊙O相切于点C,点D,E,F是⊙O上三个点,EF∥AB,若EF=2 ![]() ,则∠EDC的度数为( )
,则∠EDC的度数为( )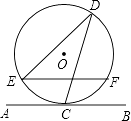
A.60°
B.90°
C.30°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________________ ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com