
【题目】如图,在⊿OAB中,∠OAB=90°.OA=AB=6.将⊿OAB绕点O逆时针方向旋转90°得到⊿OA1B1
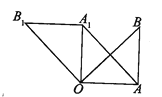
(1)线段A1B1的长是 ∠AOA1的度数是
(2)连结AA1,求证:四边形OAA1B1是平行四边形 ;
(3)求四边形OAA1B1的面积 .
【答案】(1)6,90![]() ;(2)见解析;(3)36
;(2)见解析;(3)36
【解析】
(1)根据旋转的性质即可直接求解;
(2)根据旋转的性质以及平行线的判定定理证明B1A1∥OA且A1B1=OA即可证明四边形OAA1B1是平行四边形;
(3)利用平行四边形的面积公式求解.
解:(1)由旋转的性质可知:A1B1=AB=6,∠AOA1=90°.
故答案是:6,90°;
(2)∵A1B1=AB=6,OA1=OA=6,∠OA1B1=∠OAB=90°,∠AOA1=90°,
∴∠OA1B1=∠AOA1,A1B1=OA,
∴B1A1∥OA,
∴四边形OAA1B1是平行四边形;
(3)S=OAA1O=6×6=36.
即四边形OAA1B1的面积是36.
故答案为(1)6,90![]() ;(2)见解析;(3)36.
;(2)见解析;(3)36.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,E为BC边的延长线上一点,CE=1,连接AE,与CD交于点F,连接BF并延长与线段DE交于点G,则BG的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,![]() 为等边三角形,点
为等边三角形,点![]() 为
为![]() 边上的一动点(点
边上的一动点(点![]() 不与
不与![]() 、
、![]() 重合),以
重合),以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() .求证:①
.求证:①![]() ,②
,②![]() ;
;

(2)如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 上的一动点(点
上的一动点(点![]() 不与
不与![]() 、
、![]() 重合),以
重合),以![]() 为边作等腰
为边作等腰![]() ,
,![]() (顶点
(顶点![]() 、
、![]() 、
、![]() 按逆时针方向排列),连接
按逆时针方向排列),连接![]() ,类比题(1),请你猜想:①
,类比题(1),请你猜想:①![]() 的度数;②线段
的度数;②线段![]() 、
、![]() 、
、![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(3)如图3,在(2)的条件下,若![]() 点在
点在![]() 的延长线上运动,以
的延长线上运动,以![]() 为边作等腰
为边作等腰![]() ,
,![]() (顶点
(顶点![]() 、
、![]() 、
、![]() 按逆时针方向排列),连接
按逆时针方向排列),连接![]() .
.
①则题(2)的结论还成立吗?请直接写出,不需论证;
②连结![]() ,若
,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的学生除了体育课要进行体育锻炼外,寒暑假期间还要自己抽时间进行体育锻炼,为了了解同学们假期体育锻炼的情况,开学时体育老师随机抽取了部分同学进行调查,按锻炼的时间x(分钟)分为以下四类:A类(![]() ),B类(
),B类(![]() ),C类(
),C类(![]() ),D类(
),D类(![]() ),对调查结果进行整理并绘制了如图所示的不完整的折线统计图和扇形统计图,请结合图中的信息解答下列各题:
),对调查结果进行整理并绘制了如图所示的不完整的折线统计图和扇形统计图,请结合图中的信息解答下列各题:
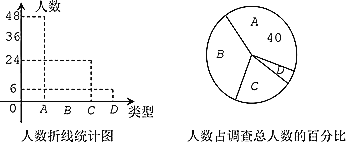
(1)扇形统计图中D类所对应的圆心角度数为 ,并补全折线统计图;
(2)现从A类中选出两名男同学和三名女同学,从以上五名同学中随机抽取两名同学进行采访,请利用画树状图或列表的方法求出抽到的学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠BCD=90°,∠B=45°,DE⊥AC于E交AB于F,若BC=2CD,AE=2,则线段BF=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰![]() 中,
中,![]() ,作
,作![]() 的外接圆⊙O.
的外接圆⊙O.
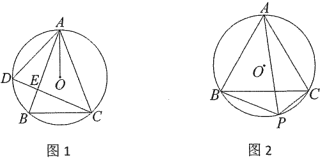
(1)如图1,点![]() 为
为![]() 上一点(不与A、B重合),连接AD、CD、AO,记
上一点(不与A、B重合),连接AD、CD、AO,记![]() 与
与![]() 的交点为
的交点为![]() .
.
①设![]() ,若
,若![]() ,请用含
,请用含![]() 与
与![]() 的式子表示
的式子表示![]() ;
;
②当![]() 时,若
时,若![]() ,求
,求![]() 的长;
的长;
(2)如图2,点![]() 为
为![]() 上一点(不与B、C重合),当BC=AB,AP=8时,设
上一点(不与B、C重合),当BC=AB,AP=8时,设![]() ,求
,求![]() 为何值时,
为何值时,![]() 有最大值?并请直接写出此时⊙O的半径.
有最大值?并请直接写出此时⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全教育,某校组织了“防溺水”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元;购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)求购买1副乒乓球拍和1副羽毛球拍各需多少元;
(2)若学校购买乒乓球拍和羽毛球拍共30幅,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com