
分析 利用描点法画出两函数图象得到它们的交点坐标,再利用代入法解方程组,然后比较交点坐标与方程组的解,可得到方程组的解就是两个相应的一次函数图象的交点坐标.
解答 解:如图,y=2x与y=x+2的图象,它们有交点,交点坐标位(2,4);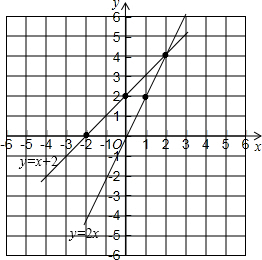
$\left\{\begin{array}{l}{y=2x①}\\{y=x+2②}\end{array}\right.$,
把①代入②得2x=x+2,解得x=2,
把x=2代入①得y=4,
所以方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,
比较交点坐标与方程组的解,得到方程组的解就是两个相应的一次函数图象的交点坐标.
点评 本题考查了一次函数与二元一次方程组:方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.


科目:初中数学 来源: 题型:解答题
 (1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号
(1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
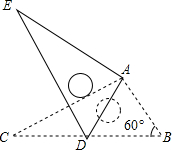 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com