
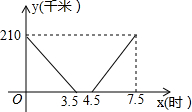
 甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离y(千米)与时间t(时)的关系如图所示,根据所提供的信息,回答下列问题:
甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离y(千米)与时间t(时)的关系如图所示,根据所提供的信息,回答下列问题:分析 (1)根据函数图象通过是信息可知,4.5-3.5=1,由此得出货车在乙地卸货停留的时间;
(2)比较货车往返所需的时间,即可得出货车往返速度的大小关系,根据路程除以时间即可求得速度.
解答 解:(1)∵4.5-3.5=1(小时),
∴货车在乙地卸货停留了1小时;
(2)∵7.5-4.5=3<3.5,
∴货车返回速度快,
∵$\frac{210}{7.5-4.5}$=70(千米/时),
∴返回速度是70千米/时.
点评 本题主要考查了函数图象,对于一个函数,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.解决问题的关键是从函数图象中获取关键的信息.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )
如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )| A. | AD=BD | B. | OC=2CD | C. | ∠CAD=∠CBD | D. | ∠OCA=∠OCB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
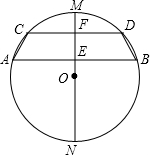 如图,在⊙O中,弦AB∥CD,直径MN⊥AB且分别交AB、CD于E、F,下列4个结论:①AE=BE;②CF=DF;③AC=BD;④MF=EF.其中正确的有( )
如图,在⊙O中,弦AB∥CD,直径MN⊥AB且分别交AB、CD于E、F,下列4个结论:①AE=BE;②CF=DF;③AC=BD;④MF=EF.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
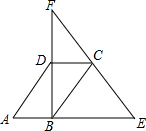 已知,如图,CD是Rt△△FBE的中位线,A是EB延长线上一点,且AB=$\frac{1}{2}$BE.
已知,如图,CD是Rt△△FBE的中位线,A是EB延长线上一点,且AB=$\frac{1}{2}$BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型节能电动车 | B型节能电动车 | |
| 进货价格(万元/辆) | 0.55 | 0.7 |
| 销售价格(万元/辆) | 2016年的销售价格 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com