
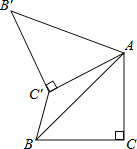
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到
,将△ABC绕点A顺时针方向旋转60°到![]() 的位置,连接
的位置,连接![]() ,则
,则![]() 的长为( ).
的长为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
【答案】A
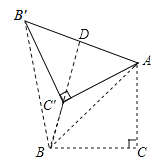
【解析】分析:连接BB′,根据旋转的性质可得AB=AB′,判断出△ABB′是等边三角形,根据等边三角形的三条边都相等可得AB=BB′,然后利用“边边边”证明△ABC′和△B′BC′全等,根据全等三角形对应角相等可得∠ABC′=∠B′BC′,延长BC′交AB′于D,根据等边三角形的性质可得BD⊥AB′,利用勾股定理列式求出AB,然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D,然后根据BC′=BD﹣C′D计算即可得解.
详解:如图,连接BB′.
∵△ABC绕点A顺时针方向旋转60°得到△AB′C′,∴AB=AB′,∠BAB′=60°,∴△ABB′是等边三角形,∴AB=BB′.
在△ABC′和△B′BC′中,∵AB=BB';AC'=B'C',BC'=BC',∴△ABC′≌△B′BC′(SSS),∴∠ABC′=∠B′BC′,延长BC′交AB′于D,则BD⊥AB′.
∵∠C=90°,AC=BC=![]() ,∴AB=
,∴AB=![]() =2,
=2,
∴BD=2×![]() =
=![]() ,C′D=
,C′D=![]() ×2=1,∴BC′=BD﹣C′D=
×2=1,∴BC′=BD﹣C′D=![]() ﹣1.
﹣1.
故选A.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
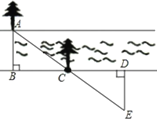
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC各顶点的坐标分A(-2,-2),B(-4,-1),C(-4,-4).

(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在
△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中
①一个角的两边分别垂直于另一角的两边,则这两个角相等或互补
②若点A在y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一象限
③半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的共有四个
④如果AD是△ABC的高,∠CAD=∠B,那么△ABC是直角三角形
正确命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为打造智慧课堂,准备集体购买一批平板电脑,原计划订购60台,每台1000元,商家表示,如果多购,可以优惠,结果校长实际订购了72台,每台减价30元,但商家获得同样多的利润.
(1)求每台平板电脑的成本是多少元?
(2)求商家的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号max﹛a , b﹜的含义为:当a≥b时, max﹛a , b﹜=a;当a<b时,max﹛a , b﹜=b.如 max﹛2 , -3﹜=2 , max﹛-4 , -2﹜=-2,则max﹛-x2+2x+3 , |x|﹜的最小值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
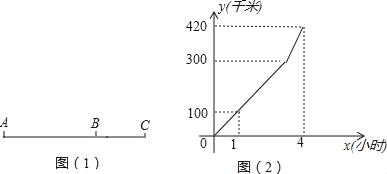
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.(1)求证: AE=AF; (2)若AG=4,AC=7,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (
(![]() ,
, ![]() )的图象与直线
)的图象与直线![]() 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
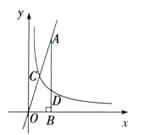
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确实一点M,使点M到C、D两点距离之和d=MC+MD,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com