
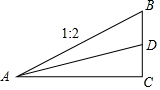
 一段斜坡路面的截面图如图所示,BC⊥AC,其中坡面AB的坡比i1=1:2,现计划削坡放缓,新坡面的坡角为原坡面坡脚的一半,求新坡面AD的坡比i2(结果保留根号)
一段斜坡路面的截面图如图所示,BC⊥AC,其中坡面AB的坡比i1=1:2,现计划削坡放缓,新坡面的坡角为原坡面坡脚的一半,求新坡面AD的坡比i2(结果保留根号) 分析 作DE⊥AB,可得∠BDE=∠BAC,即可知tan∠BAC=tan∠BDE,即$\frac{BC}{AC}$=$\frac{BE}{DE}$=$\frac{1}{2}$,设DC=2x,由角平分线性质得DE=DC=2x,再分别表示出BD、AC的长,最后由坡比定义可得答案.
解答 解:过点D作DE⊥AB于点E,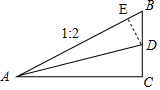
∴∠DEB=∠C=90°,
∵∠B=∠B,
∴∠BDE=∠BAC,
∴tan∠BAC=tan∠BDE,即$\frac{BC}{AC}$=$\frac{BE}{DE}$=$\frac{1}{2}$,
设DC=2x,
∵∠DAC=∠DAE,∠DEB=∠C=90°,
∴DE=DC=2x,
则BE=x,BD=$\sqrt{B{E}^{2}+D{E}^{2}}$=$\sqrt{5}$x,
∴BC=CD+BD=(2+$\sqrt{5}$)x,
∴AC=2BC=(4+2$\sqrt{5}$)x,
∴新坡面AD的坡比i2=$\frac{CD}{AC}$=$\frac{2x}{(4+2\sqrt{5})x}$=$\sqrt{5}$-2.
点评 本题主要考查解直角三角形的应用-坡角坡比问题,根据题意表示出所需线段的长度是解题的切入点和关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
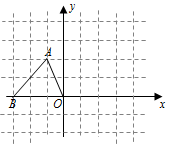 如图,O为原点,点A的坐标为(-1,2),将△ABO绕点O顺时针旋转90°后得到△CEO,则点A的对应点C的坐标为( )
如图,O为原点,点A的坐标为(-1,2),将△ABO绕点O顺时针旋转90°后得到△CEO,则点A的对应点C的坐标为( )| A. | (1,2) | B. | (2,1) | C. | (-2,1) | D. | (-2,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com