
分析 根据角平分线的性质列比例式,由此设AC=4a,AB=5a,由勾股定理列方程求出a的值,计算出斜边AB的长.
解答 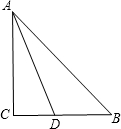 解:如图,Rt△ACB中,
解:如图,Rt△ACB中,
∵AD平分∠BAC,
∴$\frac{AC}{AB}=\frac{CD}{BD}$=$\frac{4}{5}$,
设AC=4a,AB=5a,
由勾股定理得:AB2=AC2+BC2,
∵BC=18,
∴(5a)2=(4a)2+182,
解得:a=±6,
∴AB=5a=5×6=30,
故答案为:30.
点评 本题考查了三角形的角平分线的性质,熟练掌握角平分线性质是关键;在几何计算题中,如果存在两个未知量,可以考虑得出这两个量的比,根据比值设未知数,再根据条件列等量关系式,可得出结论.


科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,AC=AD,2∠ABD+∠CBD=180°,BC=4,tanACB=$\frac{4}{7}$,△ABD的面积为20,则AD长为$\sqrt{65}$.
如图,四边形ABCD中,AC=AD,2∠ABD+∠CBD=180°,BC=4,tanACB=$\frac{4}{7}$,△ABD的面积为20,则AD长为$\sqrt{65}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AD∥BC,AB=AD+BC,AE平分∠DAB,BE平分∠CBA,点F在AB上,且AF=AD.若AE=5,BE=4,则四边形ABCD的面积为20.
如图,AD∥BC,AB=AD+BC,AE平分∠DAB,BE平分∠CBA,点F在AB上,且AF=AD.若AE=5,BE=4,则四边形ABCD的面积为20.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们经常利用图形描述问题和分析问题.借助直观的几何图形,把问题变得简明、形象,有助于探索解决问题的思路.
我们经常利用图形描述问题和分析问题.借助直观的几何图形,把问题变得简明、形象,有助于探索解决问题的思路.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(10,0)、C的坐标为(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是以OD为腰的等腰三角形时,点P的坐标为(2,4)或(8,4)或(3,4).
如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(10,0)、C的坐标为(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是以OD为腰的等腰三角形时,点P的坐标为(2,4)或(8,4)或(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com