
��ͼ1������ABCD�У�AB=21��AD=12��E��CD���ϵ�һ�㣬CE=5��M��BC���ϵ��е㣬����P�ӵ�A��������AB����ÿ��1����λ���ȵ��ٶ����յ�B�˶�������PM.�趯��P���˶�ʱ����t��.
��1�����߶�AE�ij���
��2������ADE���PBM����ʱ����t��ֵ��
��3����ͼ2������EP������P��PH��AE��H���ٵ�EPƽ���ı���PMEH�����ʱ����t��ֵ������PEΪ�Գ������߶�BC����Գ�ͼ��B��C�䣬���߶�B��C�����߶�AE�й�����ʱ��д��t��ȡֵ��Χ��ֱ��д���𰸣���
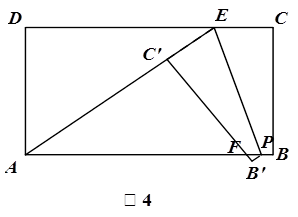
��1��AE=20����2��t=13��t=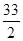 ����3����t=
����3����t=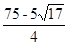 ��
��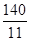 ��t��20��
��t��20��
�������������(1)��ֱ��������ADE�У���֪AD=12,DE=16,���ݹ��ɶ��������AE��ֵ����2��������������ۣ�һ������DAE=��PMBʱ���������������ε����ʣ����������εĶ�Ӧ�ߵı����.�������t��ֵ����������DAE=��MPBʱ�������������ε����ʼ������t��ֵ.(3)�ٸ�������ó�S��EHP=S��EMP�����t������ֵ���ٸ���t��ȡֵ��Χ�������t��ֵ���ڸ���PEΪ�Գ������߶�BC����Գ�ͼ��B��C�䣬����B�����߶�AE��ʱ����ͼ3��ʾ���ɹ��ɶ������EB��=13,AB��=7,���������֤�á�AB��N���ADE���ƣ��������������ζ�Ӧ�ߵı���ȣ������AN=5.6,NB��=4.2,��PN=t-5.6,PB��=21-t,�ٸ��ݹ��ɶ��������t��ֵΪ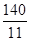 .����C�����߶�AE��ʱ����ͼ4����AC��=20-5=15,��֤��AC��F���ADE���ƣ��ɷֱ����AF,C��F��ֵ���ڡ�PFB���У����ù��ɶ�������PF��ֵ���Ӷ����AP��ֵ�������t��ֵ��������
.����C�����߶�AE��ʱ����ͼ4����AC��=20-5=15,��֤��AC��F���ADE���ƣ��ɷֱ����AF,C��F��ֵ���ڡ�PFB���У����ù��ɶ�������PF��ֵ���Ӷ����AP��ֵ�������t��ֵ��������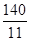 ��t��20.
��t��20.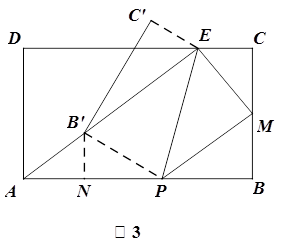
�����������1����ABCD�Ǿ��Σ����D=90�㣬��AE2=AD2+DE2����AD=12��DE=16����AE=20��
��2���ߡ�D=��B=90�㣬���ADE���PBM����ʱ�������ֿ��ܣ�
����DAE=��PMBʱ����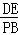 =
=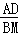 ����
����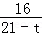 =
=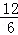 ����ã�t=13��
����ã�t=13��
����DAE=��MPBʱ����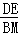 =
=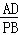 ����
����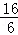 =
=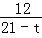 �����t=
�����t=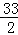 ��
��
��3����������ã�S��EHP=S��EMP��
��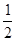 ��
��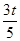 ����20��
����20��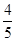 t��=
t��=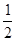 ��12����5+21��t����
��12����5+21��t����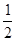 ��6����21��t����
��6����21��t����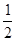 ��6��5��
��6��5��
��ã�t=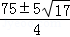 ��
��
��0��t��21��
��t=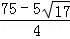 ��
��
�ڸ�������ã�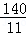 ��t��20��
��t��20��
���㣺1�����ɶ�����2�����������ε��ж������ʣ�3����ԳƵ�����.


 �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ,����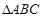 ��,
��, ,D��BC��һ��,��
,D��BC��һ��,��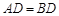 .
.
��1����֤��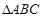 ��
�� ��
��
��2���� ,
, ,��BC�ij���
,��BC�ij���
��3����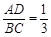 ,��
,��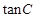 ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����E�Ǿ���ABCD��CD����һ�㣬��BCE��BE�۵�Ϊ��BFE,��F����AD��.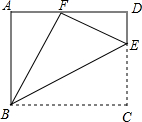
(1)��֤����ABF�ס�DFE
(2)����BEFҲ���ABF���ƣ������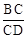 ��ֵ .
��ֵ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����6��8������ͼ�У�ÿ��С�����α߳���Ϊ1����O�͡�ABC�Ķ����ΪС�����εĶ���.
����OΪλ�����ģ�������ͼ������A��B��C�䣬ʹ��A��B��C��͡�ABCλ�ƣ���λ�Ʊ�Ϊ1��2
�����Ӣ��е�AA�䣬���ı���AA��C��C���ܳ�.������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����ͼ��������ABCD�ı߳�Ϊa��BM��DN�ֱ�ƽ�������ε�������ǣ������� ��MAN=45�㣬����MC��NC��MN��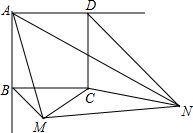
��1����գ����ABM���Ƶ��������ǡ� ��BM��DN= �����ú�a�Ĵ���ʽ��ʾ��
��2�����MCN�Ķ�����
��3�������߶�BM��DN��MN֮���������ϵ��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��AB�ǡ�O��ֱ����AC���ң�ֱ��EF������C��AD��EF�ڵ�D����DAC=��BAC. 
��1����֤��EF�ǡ�O�����ߣ�
��2����֤��AC2=AD��AB��
��3������O�İ뾶Ϊ2����ACD=300����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
��ͼ�����ⳤΪ1���������ɵĻ�ľ����ͼ����ͼ���ⳤΪ1��������ĸ�����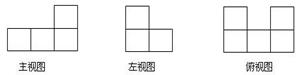
| A��5 | B��12 | C��6 | D��7 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com