
����Ŀ����ͼ����![]() �ǵȱ������Σ�
�ǵȱ������Σ� ![]() ��2
��2![]() .��
.��![]() �ӵ�
�ӵ�![]() ������������
������������![]() ��1
��1 ![]() ���ٶ��˶�������
���ٶ��˶�������![]() ��
��![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ��ͬʱ��
��ͬʱ��![]() �ӵ�
�ӵ�![]() ������
������![]() ���ӳ�����1
���ӳ�����1 ![]() ���ٶ��˶�������
���ٶ��˶�������![]() ��
��![]() .���
.���![]() ���˶�ʱ����
���˶�ʱ����![]() ��
��![]() ��.
��.
��1����֤����![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��2��ֱ��д��![]() �ij����ú�
�ij����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��3������![]() �ڱ�
�ڱ�![]() �ϣ��Ҳ����
�ϣ��Ҳ����![]() ��
��![]() �غ�ʱ����֤����
�غ�ʱ����֤����![]() �ա�
�ա�![]() .
.
��4���ڲ�������ĸ�����������߶ε������£���ͼ�е��������εĸ�������3ʱ��ֱ��д��t��ֵ�Ͷ�Ӧ�ĵ��������εĸ���.

���𰸡���1��֤����������
��2��![]() ��
��![]() ��
��
��3��֤����������
��4����t=1ʱ��ͼ����5����������������t=4ʱ��ͼ����4�����������Σ�
�������������������
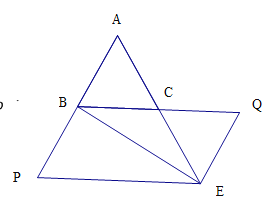
��1����ABC�ǵȱ������Σ����ݵȱ������εĶ���ã���A=��ABC=60����
����![]() ��������ֱ��ƽ����ͬλ����ȵ�����APE=��ABC=60����
��������ֱ��ƽ����ͬλ����ȵ�����APE=��ABC=60����
��Ϊ��A=��APE=60�������ݵȱ������ε��ж��ã���APE�ǵȱ������Σ�
��2�����������AE=AP=t,��t<2ʱ��CE= ![]() ����t>2ʱ��CE=
����t>2ʱ��CE= ![]() ��
�� ![]() ��
��![]() ��
��
��3��������ABC�ǵȱ������Σ��õ���AB=AC����ACB=60������Ϊ��APE�ǵȱ������Σ�
��AP=PE=AE����APE=60������AB-AP=AC-AE����BPE=��ECQ=120�������ݵ���������ǵ����ã�BP=EC������AP=CQ=t������PE=CQ������SAS�ã���BPE��ECQ��
��4����t=1ʱ��ͼ����5�����������Σ� ![]()
��t=4ʱ����ͼ��ͼ����4�����������Σ� ![]()
�����������
��1������ABC�ǵȱ������Σ�
���A=��ABC=60����
��![]() ��
��
���APE=��ABC=60����
���A=��APE=60����
����APE�ǵȱ������Σ�
��2����t<2ʱ��CE= ![]() ����t>2ʱ��CE=
����t>2ʱ��CE= ![]() ��
��
��3������ABC�ǵȱ������Σ�
��AB=AC����ACB=60����
����APE�ǵȱ������Σ�
��AP=PE=AE����APE=60����
��AB-AP=AC-AE����BPE=��ECQ=120����
��BP=EC��
��AP=CQ=t��
��PE=CQ��
����BPE��ECQ��
��4����t=1ʱ��ͼ����5�����������Σ�
��t=4ʱ����ͼ��ͼ����4�����������Σ�



 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABO�У�A��B���������ֱ�Ϊ��2��4������7��2����C��G��F��E�ֱ�Ϊ��A��B����������y�ᡢx��Ĵ�����y�ᡢx��Ľ��㣮���AOB�������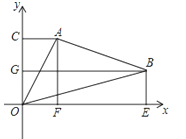
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���x2��6x+c=0��һ����Ϊ2������һ��Ϊ�� ��
A.2
B.3
C.4
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й���һ�������Ź�˾2015��Ӫҵ��ߴ�68000�ڣ�������68000�ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1����5m2n+4mn2��2mn+6m2n+3mn��
��2��2��2a��3b����3��2b��3a����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��3�·�ijʡũ��Ʒʵ�ֳ��ڶ�8 3620000��Ԫ������8 3620000�ÿ�ѧ��������ʾΪ�� ��
A.8.362��107
B.83.62��106
C.0.8362��108
D.8.362��108
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɽֲ��������A��B����������֪A��Ϊ�����Σ���Ϊ��x+y���ף���Ϊ��x��y���ף�B��Ϊ�����Σ��߳�Ϊ��x+3y���ף�
��1�����ô���ʽ��ʾA��B���������֮�Ͳ�����
��2���ָ���ʵ����Ҫ��A���������ģ������ӣ�11x��y���ף������٣�x��2y���ף����ĺ�A���ij��ȿ���350�ף������ĺ��������ܳ�֮��Ϊ980�ף�
����x��y��ֵ��
����A��ȫ����ֲC�ֻ���B��ȫ����ֲD�ֻ�����C��D���ֻ�Ͷ��ķ����������ο͵����������
C | D | |
Ͷ�루Ԫ/ƽ���ף� | 12 | 16 |
���棨Ԫ/ƽ���ף� | 18 | 26 |
�����ĺ�A��B�������εľ�����֮�ͣ���������=���橁Ͷ�룩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=![]() ��ֱ��y=��
��ֱ��y=��![]() x��
x��![]() ����A��B���㣬��֪��B�ĺ�������4��ֱ��y=��
����A��B���㣬��֪��B�ĺ�������4��ֱ��y=��![]() x��
x��![]() ��x��y��Ľ���ֱ�ΪA��C����P����������һ���㣮
��x��y��Ľ���ֱ�ΪA��C����P����������һ���㣮

��1���������ߵĽ���ʽ��
��2������P��ֱ��y=��![]() x��
x��![]() �Ϸ�������PAC����������
�Ϸ�������PAC����������
��3����M�������߶Գ����ϵ�һ�㣬�Ե�A��B��P��MΪ������ı����ܷ��Ϊƽ���ı��Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com