
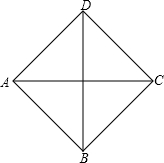
 如图,在一块对角线分别为6米、8米的菱形草地ABCD的四个顶点处,各居住着一只蚂蚁,居住在A处的蚂蚁准备沿A→B→C→D→A拜访在B、C、D三个顶点蚂蚁之后,再回到自己的住处,它的总路程为( )
如图,在一块对角线分别为6米、8米的菱形草地ABCD的四个顶点处,各居住着一只蚂蚁,居住在A处的蚂蚁准备沿A→B→C→D→A拜访在B、C、D三个顶点蚂蚁之后,再回到自己的住处,它的总路程为( )| A、14米 | B、20米 | C、24米 | D、28米 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:填空题
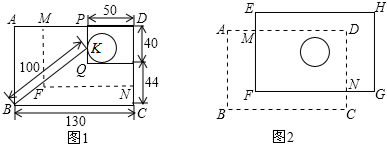
一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上。木工师傅想到了一个巧妙的办法,他测量了PQ与圆洞的切点K到点B的距离及相关数据(单位:cm)后,从点N沿折线NF-FM(NF∥BC,FM∥AB)切割,如图1所示。图2中的矩形EFGH是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠、无缝隙、不计损耗),则CN,AM的长分别是 .

查看答案和解析>>
科目:初中数学 来源:2011年河北省唐山市玉田县八年级第一学期期中考试数学卷 题型:解答题
为了美化环境,在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块:⑴分割后的整个图形必须是轴对称图形;⑵四块图形形状相同;⑶四块图形面积相等.现已有两种不同的分法:⑴分别作两条对角线(如图中的图1);⑵过一条边的四等分点作这边的垂线段(图2)(图2中两个图形的分割看作同一方法).请你按照上述三个要求,分别在下面两个正方形中给出另外两种不同的分割方法.(正确画图,不写画法)


|


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com