�⣺��1����������y=ax
2+4x+5����A��-1��0����
��a=-1��
��Գ��᷽��Ϊ

��
��2���ߵ�AΪ��-1��0������BΪ��2��9����
��ֱ��AB�Ľ���ʽΪy=3x+3��
������֪��P������Ϊ��2��m����
���D��������
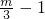
��m����
��S=

PD•|m|=

��2-

+1��•|m|=��

-
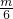
��•|m|
��S��m�ĺ�����ϵʽΪ

��

��3����ͼ������E����x=2�ĶԳƵ�E�䣬������E����x��ԳƵĵ�E''��
����E��E''��x���ڵ�M������EM��F��M�غϣ���
���Q�˶������·��Ϊ��E��F��M����E�����У���M������Ϊ��2��0����
��̾���Ϊ

��
��������1������������y=ax
2+4x+5����A��-1��0������A��-1��0���������a��ֵ��������������ߵĶԳ��᷽�̣�
��2���������ֱ��AB�Ľ���ʽ�������P������Ϊ��2��m������D������Ϊ��
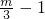
��m����Ȼ���������ε������ʽ���S��m�ĺ�����ϵʽ��
��3������E����x=2�ĶԳƵ�E�䣬������E����x��ԳƵĵ�E''������E��E''��x���ڵ�M������EM��F��M�غϣ������Q�˶������·��Ϊ��E��F��M����E�����У���M������Ϊ��2��0������̾��뼴�������
������������Ҫ������κ������ۺ����֪ʶ�������Ĺؼ��������������ȷ������ͼ�Σ������ѶȽϴ��ر��ǵ��������M������ܹؼ���

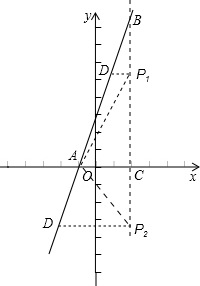
 ��֪����ƽ��ֱ������ϵxOy�У�������y=ax2+4x+5����A��-1��0�����Գ�����x�ύ�ڵ�C������ΪB��
��֪����ƽ��ֱ������ϵxOy�У�������y=ax2+4x+5����A��-1��0�����Գ�����x�ύ�ڵ�C������ΪB�� �⣺��1����������y=ax2+4x+5����A��-1��0����
�⣺��1����������y=ax2+4x+5����A��-1��0���� ��
��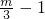 ��m����
��m���� PD•|m|=
PD•|m|= ��2-
��2- +1��•|m|=��
+1��•|m|=�� -
-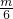 ��•|m|
��•|m| ��
��
 ��
��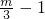 ��m����Ȼ���������ε������ʽ���S��m�ĺ�����ϵʽ��
��m����Ȼ���������ε������ʽ���S��m�ĺ�����ϵʽ��



 ��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ��y=
��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ��y= ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=