
【题目】化简计算
(1)计算: ![]() ﹣(
﹣( ![]() ﹣1)0﹣2cos30°
﹣1)0﹣2cos30°
(2)解方程: ![]() +
+ ![]() =2.
=2.
【答案】
(1)解:原式=2 ![]() ﹣1﹣2×
﹣1﹣2× ![]() =
= ![]() ﹣1
﹣1
(2)解:方程两边同时乘以(x+1)(x﹣1)得:
x+1+2x(x﹣1)=2(x+1)(x﹣1)
即:x﹣3=0
解得:x=3
经检验:x=3是原方程的解
【解析】(1)首先计算乘方,然后进行加减运算即可;(2)首先去分母化成整式方程,然后求得x的值,最后进行检验即可.
【考点精析】本题主要考查了零指数幂法则和去分母法的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(提出问题)
如图①,点![]() 、
、![]() 、
、![]() 在同一条直线上,
在同一条直线上,![]() ,
,![]() ,且
,且![]() ,
,![]() ,易证
,易证![]() ≌
≌![]() .
.
(类比探究)
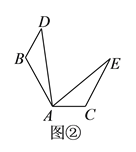
(![]() )如图②,在
)如图②,在![]() 和
和![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() .求证:
.求证:![]() ≌
≌![]() .
.
(知识应用)
(![]() )如图②,在
)如图②,在![]() 和
和![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,若
,若![]() 的度数是
的度数是![]() 的
的![]() 倍,则
倍,则![]() __________
__________![]() .
.
(数学思考)
(![]() )如图②,在
)如图②,在![]() 和
和![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,当
,当![]() ≌
≌![]() 时,
时,![]() __________.(结果用含有
__________.(结果用含有![]() 的代数式表示)
的代数式表示)
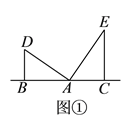
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N. 
(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
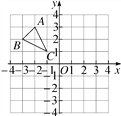
【题目】如图,格点△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC先向下平移4个单位长度,再向右平移3个单位长度,画出平移后的△A1B1C1,并写出顶点B1的坐标;
(2)作△ABC关于y轴的对称图形△A2B2C2,并写出顶点B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的象经过A(﹣1,0)、B(3,0)、N(2,3)三点,且与y轴交于点C.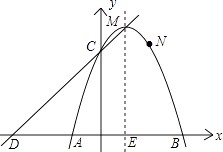
(1)求这个二次函数的解析式,并写出顶点M及点C的坐标;
(2)若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
(3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.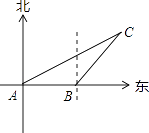
(1)说明点B是否在暗礁区域内;
(2)若继续向东航行有无触礁的危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点PQ分别是AB、AD边上的动点,则PQ+BQ的最小值是

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数 ;点P表示的数 (用含t的代数式表示)
(2)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是 .
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?
(4)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两城相距600千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为毎小时100千米,设客车出时间为t. ![]()
(1)【探究】 若客车、出租车距B城的距离分别为y1、y2 , 写出y1、y2关于t的函数关系式,并计算当y1=200千米时y2的値.
(2)【发现】 设点C是A城与B城的中点,
(Ⅰ)哪个车会先到达C?该车到达C后再经过多少小时,另一个车会到达C?
(Ⅱ)若两车扣相距100千米时,求时间t.
(3)【决策】 己知客车和出租车正好在A,B之间的服务站D处相遇,此时出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种选择返回B城的方案:
方案一:继续乘坐出租车,到达A城后立刻返回B城(设出租车调头时间忽略不计);
方案二:乘坐客车返回城.
试通过计算,分析小王选择哪种方式能更快到达B城?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com