
【题目】如图,由一段斜坡AB的高AD长为0.6米,∠ABD=30°,为了达到无障碍通道的坡道标准,现准备把斜坡改长,使∠ACD=5.71°.
(1)求斜坡AB的长;
(2)求斜坡新起点C与原起点B的距离.(精确到0.01米)(参考数据:![]() ≈1.732,tan5.71°≈0.100)
≈1.732,tan5.71°≈0.100)

 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】对于实数a,b,我们可以用min{a,b}表示a,b两数中较小的数,例如min{3,-1}=-1,min{2,2}=2. 类似地,若函数y1、y2都是x的函数,则y=min{y1, y2}表示函数y1和y2的“取小函数”.
(1)设y1=x,y2=![]() ,则函数y=min{x,
,则函数y=min{x, ![]() }的图像应该是 中的实线部分.
}的图像应该是 中的实线部分.

(2)请在下图中用粗实线描出函数y=min{(x-2)2, (x+2)2}的图像,并写出该图像的三条不同性质:

① ;
② ;
③ ;
(3)函数y=min{(x-4)2, (x+2)2}的图像关于 对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连按A2、B2、C2,得到△A2B2C2,记其面积为S2;按此规律继续下去,可得到△A2019B2019C2019,则其面积S2019=_____.
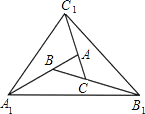
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形 ABC 的边长为 3,过点 B 的直线 l⊥AB,且△ABC 与△A′BC′关于直线 l 对称,D 为线段 BC′上一动点,则 AD+CD 的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下管道,若由甲队单独铺设,恰好在规定时间内完成;若由乙队单独铺设,需要超过规定时间15天才能完成,如果先由甲、乙两队合做10天,再由乙队单独铺设正好按时完成.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为5000元,乙队每天的施工费用为3000元,为了缩短工期以减少对居民交通的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成,那么该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上的动点,分别以AC、BC为边在AB的同侧作等边△ACD、等边△BCE,BD、AE交于点P.若AB=6,则PC的最大值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】罚球是篮球比赛中得分的一个组成部分,罚球命中率的高低对篮球比赛的结果影响很大.如图是对某球员罚球训练时命中情况的统计:

下面三个推断:①当罚球次数是500时,该球员命中次数是411,所以“罚球命中”的概率是0.822;②随着罚球次数的增加,“罚球命中”的频率总在0.812附近摆动,显示出一定的稳定性,可以估计该球员“罚球命中”的概率是0.812;③由于该球员“罚球命中”的频率的平均值是0.809,所以“罚球命中”的概率是0.809.其中合理的是( )
A.①B.②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
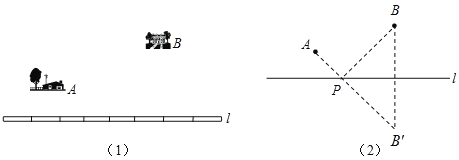
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
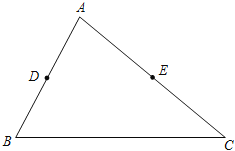
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com