练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．YC市首批一次性投放公共自行车700辆供市民租用出行，由于投入数量不够，导致出现需要租用却未租到车的现象，现将随机抽取的某五天在同一时段的调查数据汇成如下表格．
    请回答下列问题：
    时间第一天7：00-8：00第二天7：00-8：00第三天7：00-8：00第四天7：00-8：00第五天7：00-8：00
    需要租用自行车却未租到车的人数（人）15001200130013001200
    （1）表格中的五个数据（人数）的中位数是多少？
    （2）由随机抽样估计，平均每天在7：00-8：00需要租用公共自行车的人数是多少？

    分析 （1）表格中5个数据按从小到大的顺序排列后，中位数应是第3个数据；
    （2）根据平均数等于数据之和除以总个数求出平均每天需要租用自行车却未租到车的人数，再加上700即可．

    解答 解：（1）表格中5个数据按从小到大的顺序排列为1200，1200，1300，1300，1500，
    所以中位数是1300；

    （2）平均每天需要租用自行车却未租到车的人数：（1500+1200+1300+1300+1200）÷5=1300，
    ∵YC市首批一次性投放公共自行车700辆供市民租用出行，
    ∴平均每天需要租用公共自行车的人数是1300+700=2000．

    点评 本题考查了中位数，平均数以及用样本估计总体．将一组数据从小到大依次排列，把中间数据（或中间两数据的平均数）叫做中位数．平均数=总数÷总个数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．在平面直角坐标系中，点A是抛物线y=a（x-3）2+k与y轴的交点，点B是这条抛物线上的另一点，且AB∥x轴，则以AB为边的等边三角形ABC的周长为（　　）
    A．15B．18C．21D．24

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，在△ABC中，∠BAD=∠DAC，DF⊥AB，DM⊥AC，AB=16cm，AF=10cm，AC=14cm，动点E以2cm/s的速度从A点向B点运动，动点G以1cm/s的速度从C点向A点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为t．
    （1）求：AM=10cm，$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{8}{7}$；
    （2）求证：在运动过程中，无论t取何值，都有S△AED=2S△DGC；
    （3）当t取何值时，△DFE与△DMG全等；
    （4）若BD=8，则CD=7cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．方程$\frac{2}{x-1}$=$\frac{3}{x+2}$的解是x=7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

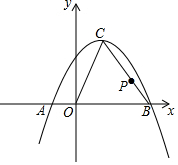    19．已知：如图，抛物线y=ax2+x+c与x轴交于点A（-1，0），B（3，0）．
    （1）试确定该抛物线的函数表达式；
    （2）已知点C是该抛物线的顶点，求△OBC的面积；
    （3）若点P是线段BC上的一动点，求OP的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

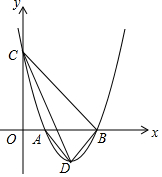    9．如图，抛物线y=a（x-1）（x-3）与x轴交于A，B两点，与y轴的正半轴交于点C，其顶点为D．
    （1）写出C，D两点的坐标（用含a的式子表示）；
    （2）设S△BCD：S△ABD=k，求k的值；
    （3）当△BCD是直角三角形时，求对应抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．矩形的长与宽分别为a、b，下列数据能构成黄金矩形的是（　　）
    A．a=4，b=$\sqrt{5}$+2B．a=4，b=$\sqrt{5}$-2C．a=2，b=$\sqrt{5}$+1D．a=2，b=$\sqrt{5}$-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

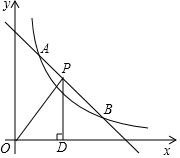    13．如图，一次函数y=-x+b与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点A（m，3）和B（3，1）．
    （1）填空：一次函数的解析式为y=-x+4，反比例函数的解析式为y=$\frac{3}{x}$；
    （2）点P是线段AB上一点，过点P作PD⊥x轴于点D，连接OP，若△POD的面积为S，求S的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知点N（a-2，3）在y轴上，则a的值为2．

    查看答案和解析>>

    同步练习册答案