
【题目】如图,△ABC是边长为6 cm的等边三角形,动点P从A出发,以3 cm/s的速度,沿A-B-C向C运动,同时,动点Q从C出发沿CA方向以1 cm/s的速度向A运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t= ____s,△APQ是直角三角形.

科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本“目标与评定”中有这样一道思考题:如图钢架中∠A=20°,焊上等边的钢条P1P2,P2P3,P3P4,P4P5…来加固钢架,若P1A=P1P2,问这样的钢条至多需要多少根?
(1)请将下列解答过程补充完整:
答案:∵∠A=20°,P1A=P1P2,∴∠P1P2A= .
又P1P2=P2P3=P3P4=P4P5,∴∠P2P1P3=P2P3P1=40°,
同理可得,∠P3P2P4=P3P4P2=60°,∠P4P3P5=P4P5P3= ,
∴∠BP4P5=∠CP5P4=100°>90°,
∴对于射线P4B上任意一点P6(点P4除外),P4P5<P5P6,
∴这样的钢架至多需要 根.
(2)继续探究:当∠A=15°时,这样的钢条至多需要多少根?
(3)当这样的钢条至多需要8根时,探究∠A的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘外卖送餐员,送餐员的月工资由底薪1000元加上外卖送单补贴![]() 送一次外卖称为一单
送一次外卖称为一单![]() 构成,外卖送单补贴的具体方案如下:
构成,外卖送单补贴的具体方案如下:
外卖送单数量 | 补贴 |
每月不超过500单 | 6 |
超过500单但不超过m单的部分 | 8 |
超过m单的部分 | 10 |
![]() 若某“外卖小哥”4月份送餐400单,则他这个月的工资总额为多少元?
若某“外卖小哥”4月份送餐400单,则他这个月的工资总额为多少元?
![]() 设5月份某“外卖小哥”送餐x单
设5月份某“外卖小哥”送餐x单![]() ,所得工资为y元,求y与x的函数关系式.
,所得工资为y元,求y与x的函数关系式.
![]() 若某“外卖小哥”5月份送餐800单,所得工资为6500元,求m的值.
若某“外卖小哥”5月份送餐800单,所得工资为6500元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a-3b|+(a+b-4)=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
(1)求a、b的值;
(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某项工程由甲乙两队合作12天可以完成,供需工程费用13800元,乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多150元。
(1)甲乙两队单独完成这项工程分别需要多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成这项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)试说明△ABC是等腰三角形;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒2cm的速度沿线段BA向点A 运动,同时动点N从点A出发以每秒1cm速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.
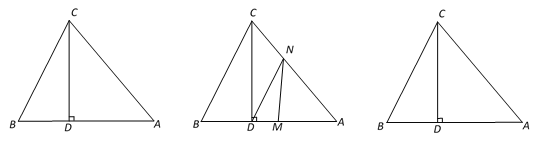
图1 图2 备用图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com