
分析 (1)运用配方法将抛物线的解析式化为y=a(x+h)2+k形式,即可得到顶点C坐标、对称轴;
(2)根据函数解析式求得A、B两点坐标,得出AB的长,最后计算△ABC的面积即可;
(3)根据点A与点B关于直线x=2对称,连接AD交直线x=2于P,则点P即为所求,PB+PD的最小值为AD长,最后根据勾股定理求得AD长,即可得出PB+PD的最小值.
解答 解:(1)∵y=-2x2+8x-4
=-2(x2-4x)-4
=-2(x2-4x+4-4)-4
=-2(x-2)2+4,
∴抛物线的顶点坐标为(2,4),对称轴为直线x=2;
(2)令y=0,则-2(x-2)2+4=0,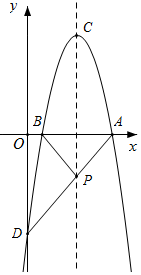
∴(x-2)2=2,
∴x-2=±$\sqrt{2}$,
∴x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$,
∴抛物线与x轴的交点坐标为A(2+$\sqrt{2}$,0),B(2-$\sqrt{2}$,0),
∴△ABC的面积=$\frac{1}{2}$×4×[(2+$\sqrt{2}$)+(2-$\sqrt{2}$)]=4$\sqrt{2}$;
(3)如图,二次函数的图象与y轴交于D点(0,-4),
点A与点B关于直线x=2对称,
连接AD交直线x=2于P,则点P即为所求,
此时,PB+PD的最小值为AD长,
∵Rt△AOD中,AD=$\sqrt{O{D}^{2}+O{A}^{2}}$=$\sqrt{{4}^{2}+(2+\sqrt{2})^{2}}$=$\sqrt{22+4\sqrt{2}}$,
∴PB+PD的最小值为$\sqrt{22+4\sqrt{2}}$.
点评 本题主要考查了抛物线与x轴的交点、待定系数法求二次函数解析式、最短路线问题,掌握二次函数的性质和图象是解题的关键.凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要涉及点关于某直线的对称点.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
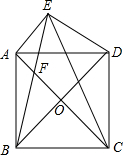 如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.
如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一次函数y=x+b的图象过点A(1,2),且与x轴相交于点B,若点P是x轴上的一点,且满足△APB是等腰三角形,则点P的坐标可以是(3,0),(2$\sqrt{2}$-1,0),(-2$\sqrt{2}$-1,0),(1,0).
如图,一次函数y=x+b的图象过点A(1,2),且与x轴相交于点B,若点P是x轴上的一点,且满足△APB是等腰三角形,则点P的坐标可以是(3,0),(2$\sqrt{2}$-1,0),(-2$\sqrt{2}$-1,0),(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
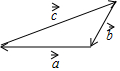 如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,那么下列结论正确的是( )
如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,那么下列结论正确的是( )| A. | $\overrightarrow{a}$$+\overrightarrow{b}$=$\overrightarrow{c}$ | B. | $\overrightarrow{b}$$+\overrightarrow{c}$=$\overrightarrow{a}$ | C. | $\overrightarrow{a}$$+\overrightarrow{c}$=$\overrightarrow{b}$ | D. | $\overrightarrow{a}$$+\overrightarrow{c}$=$-\overrightarrow{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.
如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 每段绳子长$\frac{25}{30}$米 | B. | 每段绳子占全长的$\frac{6}{7}$ | ||
| C. | 每段绳子长$\frac{6}{7}$米 | D. | 每段绳子是全长的$\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com