练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    求二次函数y=-（x+2）（x-2）的图象与x轴的交点，并画草图验证．
    考点：抛物线与x轴的交点
    专题：
    分析：抛物线与x轴交点的纵坐标为零，据此求出抛物线与x轴的交点坐标，画出函数图象即可．
    解答：解：如图：当y=0时，-（x+2）（x-2）=0，
    解得x1=-2，x2=2，
    即抛物线与x轴交点坐标为（-2，0），（2，0）．
    点评：本题考查的是抛物线与x轴的交点，根据题意画出图形，利用数形结合求解是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    化简：（
    2x2+2x
    x2-1
    -
    x2-x
    x2+1-2x
    ）÷
    x
    x+1
    ，并解答：
    （1）当x=5时，求原代数式的值；
    （2）原代数式的值能等于2吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    平面内有五个点，过每两个点作一条直线，可以作几条直线？（　　）
    A、1条、4条、8条或10条
    B、1条、5条、9条或10条
    C、1条、5条、8条或10条
    D、1条或10条

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某露天游泳池对外开放时，收入以出售门票的方式获得，每天各项开支的总成本是固定的，一天内盈利y（元）与购票进场的人数x（人）之间的函数关系如图所示．为保证游泳时的安全与卫生，管理部门对每天进入游泳池的人数进行了限制．
    根据图象回答下列问题：
    （1）管理部门规定一天内游泳池的最大容量是多少？经营者一天内的最高盈利是多少？
    （2）一天内出售多少门票时，经营者才能保证不亏损？要使一天内的盈利在600元以上，至少要出售多少张门票？
    （3）盈利为什么能取负值？-200的含义是什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

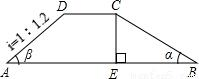    如图，水坝的横截面积是梯形ABCD，迎水坡BC的坡角α为30°，背水坡AD的坡度i，即（tanβ）为1：1.2，坝顶宽DC=2.5m，坝高4.5m．
    （1）求：坝底宽AB的长．（结果保留根号）
    （2）若把堤坝加高0.5米（整个大坝长5m，不改变坡角与坝底），需要多少土方？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：x=
    2
    		3
    -1
    ，求x2-2x+2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示是四位同学所画的数轴，其中正确的是（　　）
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列具有相反意义的量是（　　）
    A、胜二局与负三局
    B、盈利3万元与支出3万元
    C、气温升高3℃与气温为-3℃
    D、小明向东走10米与向北走10米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    二次函数y=-（x-1）2-2的顶点坐标是（　　）
    A、（-1，-2）
    B、（-1，2）
    C、（1，-2）
    D、（1，2）

    查看答案和解析>>

    同步练习册答案