
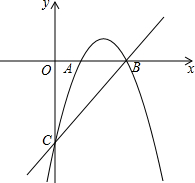
 ��ƽ��ֱ������ϵxOy�У�������y=-x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����B������Ϊ��3��0����ֱ��y=kx-3����B��C���㣮
��ƽ��ֱ������ϵxOy�У�������y=-x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����B������Ϊ��3��0����ֱ��y=kx-3����B��C���㣮���� ��1�����ݴ���ϵ�������ɵú�������ʽ��
��2����������ıȣ��ɵ�PB��PC��ֵ���������������ε��ж������ʣ��ɵ�PD�ij��������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
��3������Բ�����������У��ɵ�x��y��ֵ���ٸ����Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�Q�����꣮
��� �⣺��1����B���������y=kx-3����
3k-3=0�����k=1��
ֱ�ߵĽ���ʽΪy=x-3����x=0ʱ��y=-3����C������Ϊ��0��-3����
��B��C��������������ߵĽ���ʽ�����b=4��c=-3��
�����ߵĽ���ʽΪy=-x2+4x-3��
��2����PD��AB��D�㣬��ͼ��
��S��ABP��S��APC=2��3����PB��PC=2��3��PB��BC=2��5��
�ɡ�PBD�ס�COB����$\frac{PD}{OC}$=$\frac{PB}{BC}$�����DP=$\frac{6}{5}$��
���P���������Ϊ-$\frac{6}{5}$��
��y=-$\frac{6}{5}$ʱ��x-3=-$\frac{6}{5}$�����x=$\frac{9}{5}$��
��P�����������$\frac{9}{5}$��-$\frac{6}{5}$����
��3����Q��x��y����
�ٵ���Q��y������ʱ����|x|=1����x=��1��
��x=1ʱ��y=-x2+4x-3=0����Q�������Ϊ��1��0����
��x=-1ʱ��y=-x2+4x-3=-8����Q�������Ϊ��-1��8����
�ڵ���Q��x������ʱ����|y|=1����y=��1��
��y=1ʱ��1=-x2+4x-3�����x=2����Q�������Ϊ��2��1����
��y=-1ʱ��-1=-x2+4x-3�����x=2$��\sqrt{2}$����Q��2+$\sqrt{2}$��-1������2-$\sqrt{2}$��-1����
�������������ڡ�Q�����������У�Բ��Q������Ϊ��1��0������-1��8������2+$\sqrt{2}$��-1������2-$\sqrt{2}$��-1����
�۵���Q����������ͬʱ����ʱ����|x|=|y|��
��y=xʱ��-x2+4x-3=x���˷����⣻
��y=-xʱ��-x2+4x-3=-x�����x=$\frac{5��\sqrt{13}}{2}$����r=$\frac{5��\sqrt{13}}{2}$ʱ����Q����������ͬʱ���У�
������������r=$\frac{5��\sqrt{13}}{2}$ʱ����Q����������ͬʱ���У�
���� ���⿼���˶��κ����ۺ��⣬�������������ε��ж������ʵó�PD�ij��ǽ���ؼ�������Բ�����������еó�x��y��ֵ�ǽ���ؼ���Ҫ�������ۣ��Է���©��


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
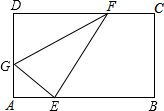 �ھ���ABCD�У�AB=5��BC=3����ͼ��ʾ�۵�����ABCD��ʹD�����ڱ�AB��һ��E�����ۺ۶˵�G��F�ֱ��ڱ�AD��DC�ϣ����ۺ۶˵�Fǡ����C���غ�ʱ��AE�ij�Ϊ1cm��
�ھ���ABCD�У�AB=5��BC=3����ͼ��ʾ�۵�����ABCD��ʹD�����ڱ�AB��һ��E�����ۺ۶˵�G��F�ֱ��ڱ�AD��DC�ϣ����ۺ۶˵�Fǡ����C���غ�ʱ��AE�ij�Ϊ1cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
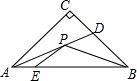 ��ͼ��ʾ��Rt��ABC�У�AC=BC=4��ADƽ�֡�BAC����E�ڱ�AB�ϣ���AE=1����P���߶�AD�ϵ�һ�����㣬��PE+PB����Сֵ����5��
��ͼ��ʾ��Rt��ABC�У�AC=BC=4��ADƽ�֡�BAC����E�ڱ�AB�ϣ���AE=1����P���߶�AD�ϵ�һ�����㣬��PE+PB����Сֵ����5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | ��4 | C�� | 8 | D�� | ��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 50=05 | B�� | |-5|=-5 | C�� | 6-1=$\frac{1}{6}$ | D�� | $\sqrt{16}$=��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC��
��ͼ����֪��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | �ٶ� | B�� | �ڶ� | C�� | �۶� | D�� | �ܶ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com