
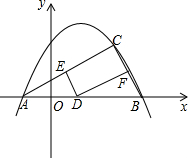 如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.
如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.分析 (1)因为抛物线与x轴交于(-1,0)(4,0),可以假设y=a(x+1)(x-4),由题意a=-$\frac{1}{2}$代入整理即可求出b、c.
(2)①利用待定系数法思想求出点C坐标,利用勾股定理的逆定理证明∠ACB=90°,由此即可解决问题;
②根据相似三角形的判定与性质,可得$\frac{ED}{BC}$=$\frac{AD}{AB}$,$\frac{DF}{AC}$=$\frac{BD}{AB}$,根据等式的性质,可得$\frac{ED}{BC}$+$\frac{DF}{AC}$,再根据等量代换,可得答案.
解答 (1)解:因为抛物线与x轴交于(-1,0)(4,0),可以假设y=a(x+1)(x-4)
∵a=-$\frac{1}{2}$,
∴y=-$\frac{1}{2}$(x+1)(x-4)
即y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)①证明:把C(m,m-1)代入y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2得
m-1=-$\frac{1}{2}$m2+$\frac{3}{2}$m+2,
∴m1=-2,m2=3,
∵C在第一象限,
∴$\left\{\begin{array}{l}{m>0}\\{m-1>0}\end{array}\right.$,∴m>1,
∴m=-2(不符合题意,舍),m=3,
∴C的坐标是(3,2),
∵BC∥DE DF∥AC,
∴四边形DECF是平行四边形,
∵AB2=25 AC2=20 BC2=5
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴四边形?BECF是矩形.
②∵DE∥BC,
∴△AED∽△ACB,
∴$\frac{ED}{BC}$=$\frac{AD}{AB}$ (1).
同理,得
$\frac{DF}{AC}$=$\frac{BD}{AB}$ (2),
(1)+(2)得
$\frac{ED}{BC}$+$\frac{DF}{AC}$=$\frac{AD+BD}{AB}$=1,
∵AC=2$\sqrt{5}$,BC=$\sqrt{5}$,CF=ED,
∴$\frac{ED}{\sqrt{5}}$+$\frac{DF}{2\sqrt{5}}$=1,
即2ED+DF=2$\sqrt{5}$,
∴ED+DF+FC=2$\sqrt{5}$,
∴DE、DF、CF的长度之和不变化,ED+DF+FC=2$\sqrt{5}$.
点评 本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)①的关键是利用矩形的判定,又利用了勾股定理机勾股定理的逆定理;解②的关键是利用相似三角形的判定与性质得出关于$\frac{ED}{BC}$=$\frac{AD}{AB}$,$\frac{DF}{AC}$=$\frac{BD}{AB}$,又利用了等式的性质,等量代换.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
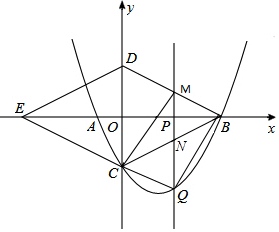 如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点,与y轴交于点C,连接BC,以BC为一边,点O为对称中心做菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点,与y轴交于点C,连接BC,以BC为一边,点O为对称中心做菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
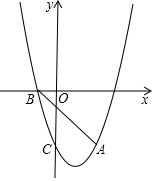 如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com