
【题目】如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.
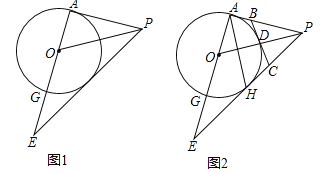
(1)求证:直线PE是⊙O的切线;
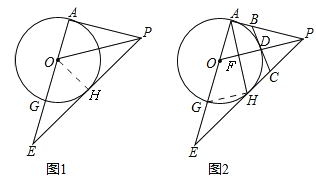
(2)在图2中,设PE与⊙O相切于点H,连结AH,点D是⊙O的劣弧![]() 上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=
上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=![]() ,求EH的长.
,求EH的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)作OH⊥PE,由PO是∠APE的角平分线,得到∠APO=∠EPO,判断出△PAO≌△PHO,得到OH=OA,用“圆心到直线的距离等于半径”来得出直线PE是⊙O的切线;
(2)先利用切线的性质和△PBC的周长为4求出PA=2,再用三角函数求出OA,AG,然后用三角形相似,得到EH=2EG,AE=2EH,用勾股定理求出EG,最后用切割线定理即可.
试题解析:(1)如图1,作OH⊥PE,∴∠OHP=90°,∵∠PAE=90,∴∠OHP=∠OAP,∵PO是∠APE的角平分线,∴∠APO=∠EPO,在△PAO和△PHO中,∵∠OHP=∠OAP,∠OPH=∠OPA,OP=OP,∴△PAO≌△PHO,∴OH=OA,∵OA是⊙O的半径,∴OH是⊙O的半径,∵OH⊥PE,∴直线PE是⊙O的切线.
(2)如图2,连接GH,∵BC,PA,PB是⊙O的切线,∴DB=DA,DC=CH,∵△PBC的周长为4,∴PB+PC+BC=4,∴PB+PC+DB+DC=4,∴PB+AB+PC+CH=4,∴PA+PH=4,∵PA,PH是⊙O的切线,∴PA=PH,∴PA=2,由(1)得,△PAO≌△PHO,∴∠OFA=90°,∴∠EAH+∠AOP=90°,∵∠OAP=90°,∴∠AOP+∠APO=90°,∴∠APO=∠EAH,∵tan∠EAH=![]() ,∴tan∠APO=
,∴tan∠APO=![]() =
=![]() ,∴OA=
,∴OA=![]() PA=1,∴AG=2,∵∠AHG=90°,∵tan∠EAH=
PA=1,∴AG=2,∵∠AHG=90°,∵tan∠EAH=![]() =
=![]() ,∵△EGH∽△EHA,∴
,∵△EGH∽△EHA,∴![]() =
=![]() =
=![]() ,∴EH=2EG,AE=2EH,∴AE=4EG,∵AE=EG+AG,∴EG+AG=4EG,∴EG=
,∴EH=2EG,AE=2EH,∴AE=4EG,∵AE=EG+AG,∴EG+AG=4EG,∴EG=![]() AG=
AG=![]() ,∵EH是⊙O的切线,EGA是⊙O的割线,∴
,∵EH是⊙O的切线,EGA是⊙O的割线,∴![]() =EG×EA=EG×(EG+AG)=
=EG×EA=EG×(EG+AG)=![]() =
=![]() ,∴EH=
,∴EH=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一件商品按成本价提高40%后标价,再打8折(标价的80%)销售,售价为240元,设这件商品的成本价为x元,根据题意,下面所列的方程正确的是( )
A. 40%x·80%=240
B. (1+40%)x·80%=240
C. 240×40%×80%=x
D. 40%x=240×80%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种药品说明书上标明保存温度是(20±3)0C,则该药品在( )范围内保存最合适.
A. 170C~200C B. 200C ~230C C. 170C ~230C D. 170C ~240C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式变形不正确的是( )
A. 由x=y,得到x+2=y+2
B. 由2a﹣3=b﹣3,得到2a=b
C. 由m=n,得到2am=2an
D. 由am=an,得到m=n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com