
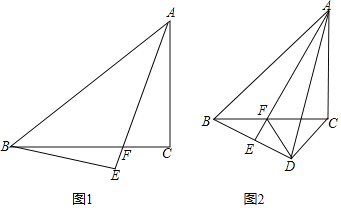
【题目】如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,在△ABE中,∠AEB=90°,AE与BC交于点F.
(1)若∠BAE=30°,BF=2![]() ,求BE的长;
,求BE的长;
(2)如图2,D为BE延长线上一点,连接AD、FD、CD,若AB=AD,∠ACD=135°,求证:BD+BF=AF.
【答案】(1)BE=1+![]() ;(2)见解析
;(2)见解析
【解析】
(1)如图1中,作FE⊥BA于E.在Rt△BEF中,求出BE=EF=2,在Rt△AEF中,求得AE=2![]() ,再在Rt△ABE中,根据BE=
,再在Rt△ABE中,根据BE=![]() AB即可解决问题;
AB即可解决问题;
(2)延长AC交BD的延长线于H.只要证明△BCH≌△ACF,△CDF≌△CDH,AE垂直平分线段BD,即可解决问题;
(1)解:如图1中,作FE⊥BA于E.
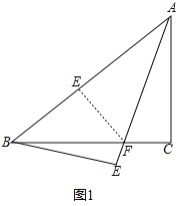
∵CA=CB,∠C=90°,
∴∠ABC=45°,∵∠BEF=90°,
∴△BEF是等腰直角三角形,
∵BF=2![]() ,
,
∴BE=EF=2,
在Rt△AEF中,∵∠EAF=30°,
∴AE=![]() EF=2
EF=2![]() ,
,
∴AB=2+2![]() ,
,
在Rt△ABE中,∵∠BAE=30°,
∴BE=![]() AB=1+
AB=1+![]() .
.
(2)证明:如图2中,延长AC交BD的延长线于H.
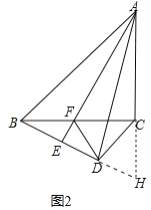
∵∠BEF=∠ACF=90°,∠BFE=∠AFC,
∴∠HBC=∠CAF,∵CB=CA,∠BCH=∠ACF,
∴△BCH≌△ACF,
∴AF=BH,CF=CH,
∵∠ACD=135°,∠ACB=90°,
∴∠ECD=∠HCD=45°,
∵CD=CD,
∴△CDF≌△CDH,
∴DF=DH,
∵AB=AD,AE⊥BD,
∴BE=ED,
∴AE垂直平分线段BD,
∴FB=FD=DH,
∴AF=BH=BD+DH=BD+BF,
∴BD+BF=AF.


科目:初中数学 来源: 题型:
【题目】小李通过对某地区1998年至2000年快餐公司发展情况的调查,制成了该地区快餐公司个数情况的条形图如图所示,和快餐公司盒饭年销量的平均数情况条形图,利用这些信息解答下列问题:


(1)1999年该地区销售盒饭共 万盒;
(2)该地区盒饭销量最大的年份是 个,这一年的年销量是 万盒;
(3)这三年中该地区每年平均销售盒饭多少万盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台摄制组乘船往返于A码头和B码头进行拍摄,在A、B两码头间设置拍摄中心C.在往返过程中,假设船在A、B、C处均不停留,船离开B码头的距离s(千米)与航行的时间t(小时)之间的函数关系式如图所示.根据图象信息,解答下列问题:
(1)求船从B码头返回A码头时的速度及返回时s关于t的函数表达式.
(2)求水流的速度.
(3)若拍摄中心C设在离A码头12千米处,摄制组在拍摄中心分两组拍摄,其中一组乘橡皮艇漂流到B码头处,另一组同时乘船到达A码头后马上返回,求两摄制组相遇时离拍摄中心C的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BD,∠BAD=50°,∠C=30°.
(1)求∠BAC的度数;
(2)取AD的中点E,连接BE并延长交AC于点F.求证:AB=BF.

查看答案和解析>>
科目:初中数学 来源: 题型:
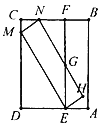
【题目】如图,矩形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,过点
边上,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点
于点![]() ,易得矩形
,易得矩形![]() .将矩形
.将矩形![]() 绕着点
绕着点![]() 逆时针旋转,使点
逆时针旋转,使点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,点
上,点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,
上,![]() 的对应边
的对应边![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;(提示:连接
;(提示:连接![]() ,
,![]() )
)
(2)当旋转角为30°时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
图1,等腰△ABC中,AB=AC,∠BAC=120°,过点A作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°;于是
∠BAC=60°;于是![]() =
=![]() =
=![]() ;
;

(1)迁移应用:
如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.求证:CD=![]() AD+BD;
AD+BD;
(2)拓展延伸
如图图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.若AE=5,CE=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐山独峰,倚天独立.身高1.6米的小明(GF)和身高1.8米的爸爸(HE)前去游览,山腰处的一棵缀满红叶的枫树(A)吸引了他们的目光,已知小明的仰角为30°,爸爸的仰角为45°,若小明与爸爸之间(EF)相距6米,求枫树(A)与地面的距离(AD)为多少米?(参考数据:![]() 1.41,
1.41,![]() 1.73,结果保留一位小数.)
1.73,结果保留一位小数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
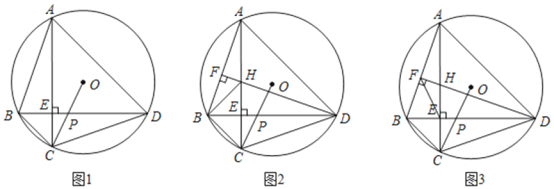
(1)如图1,求证:![]() ;
;
(2)如图2,作![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com