
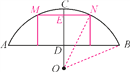
【题目】如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2 m,拱高CD为2.4 m.
(1)求拱桥的半径;
(2)现有一艘宽3 m,船舱顶部为长方形并高出水面2 m的货船要经过这里,问此货船能顺利通过拱桥吗?

【答案】(1)拱桥的半径为3.9 m;(2)此货船能顺利通过拱桥.
【解析】 试题分析:(1)连接OB,根据垂径定理求出BD,设OB=OC=r,再在Rt△BOD中利用勾股定理求出r;(2)作出拱桥下的矩形,交拱桥于M,N,交CD于E,连接ON,通过求距离水面2米高处即ED长为2时,桥有多宽,即MN的长,当货船顶部宽度大于MN则货船不能通过,当货船顶部宽度小于等于MN则货船能通过.
解:(1)连接OB.
∵OC⊥AB,∴D为AB的中点.
∴BD=![]() AB=3.6(m).
AB=3.6(m).
设OB=OC=r,则OD=(r-2.4)m.
在Rt△BOD中,OB2=OD2+BD2,即r2=(r-2.4)2+3.62,解得r=3.9.
∴拱桥的半径为3.9 m.
(2)作出拱桥下的矩形,交拱桥于M,N,交CD于E,连接ON.
∵CD=2.4 m,DE=2 m,
∴CE=CD-DE=0.4(m).
∴OE=OC-CE=3.9-0.4=3.5(m).
在Rt△OEN中,EN=![]() =
=![]() =
=![]() (m2),
(m2),
∵OD⊥MN,
∴MN=2EN=2×![]() ≈3.44 m>3 m.
≈3.44 m>3 m.
∴此货船能顺利通过拱桥.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.

(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,求证:AB=4PD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解参加运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄.就这个问题来说,下面说法中正确的是( )
A.2000名运动员是总体
B.每个运动员是个体
C.100名运动员是抽取的一个样本
D.抽取的100名运动员的年龄是样本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于轴对称位置变换,说法正确的有( )
①对应线段平行且相等;
②对应点的连线被对称轴垂直平分;
③对应角相等;
④轴对称得到的图形与原图形全等.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2014年投入教育经费200万元,2016年投入教育经费242万元.
(1)求2014年至2016年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2017年该地区将投入教育经费多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com