
【题目】如图1,已知:直线y=![]() x﹣3分别交x轴于A,交y轴于B,抛物线C1:y=x2+4x+b的顶点D在直线AB上.
x﹣3分别交x轴于A,交y轴于B,抛物线C1:y=x2+4x+b的顶点D在直线AB上.
(1)求抛物线C1的解析式;
(2)如图2,将抛物线C1的顶点沿射线DA的方向平移得抛物线C2 , 抛物线C2交y轴于C,顶点为E,若CE⊥AB,求抛物线C2的解析式;
(3)如图3,将直线AB沿y轴正方向平移t(t>0)个单位得直线l,抛物线C1的顶点在直线AB上平移得抛物线C3 , 直线l和抛物线C3相交于P、Q,求当t为何值时,PQ=3![]() ?
?
【答案】解:(1)由y=x2+4x+b=(x+2)2﹣4+b,
∴顶点D的坐标(﹣2,﹣4+b),
代入y=![]() x﹣3得:﹣4+b=
x﹣3得:﹣4+b=![]() ×(﹣2)﹣3,
×(﹣2)﹣3,
解得:b=0,
∴抛物线C1的解析式为:y=x2+4x;
(2)∵抛物线C1的顶点沿射线DA的方向平移得抛物线C2 ,
∴抛物线C1的向右平移a个单位的同时向上平移![]() a个单位,
a个单位,
∵y=x2+4x=(x+2)2﹣4,
∴抛物线C2的解析式为:y=(x+2﹣a)2﹣4+![]() ,
,
∴E(﹣2+a,﹣4+![]() ),
),
令x=0,则y=a2﹣![]() a,
a,
∵CE⊥AB,
∴直线CE的斜率为﹣2,
∴直线CE为:y=﹣2x+a2﹣![]() a,
a,
∴﹣4+![]() =﹣2(﹣2+a)+a2﹣
=﹣2(﹣2+a)+a2﹣![]() a,
a,
解得:a=2(舍去),a=4,
∴抛物线C2的解析式为:y=(x﹣2)2﹣2;
(3)∵PQ的长与C3移动到的位置无关,
∴当抛物线C3的顶点在y轴时,抛物线的解析式为:y=x2﹣3,
∵直线AB沿y轴正方向平移t(t>0)个单位得直线l,
∴直线l的解析式为:y=![]() x﹣3+t,
x﹣3+t,
解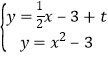 ,得:x1=
,得:x1=![]() ,x2=
,x2=![]() ,
,
∵x1﹣x2=![]() ,
,
∴PQ2=(![]() )2+(
)2+(![]() )2=
)2=![]() ,
,
∵PQ=3![]() ,
,
∴PQ2=45,
∴![]() =45,
=45,
解得t=![]() ,
,
∴当t=![]() 时,P、Q之间的距离为3
时,P、Q之间的距离为3![]() .
.
【解析】(1)根据抛物线的解析式转化为顶点式,求得顶点D的坐标,把D的坐标代入,直线的解析式即可求得b的值进而求得抛物线C1的解析式;
(2)先得出抛物线C2的解析式为:y=(x+2﹣a)2﹣4+![]() , 求得顶点E的坐标,令x=0,求得y=a2﹣
, 求得顶点E的坐标,令x=0,求得y=a2﹣![]() a,由于CE⊥AB,所以直线CE的斜率为﹣2,进而求得直线CE为:y=﹣2x+a2﹣a,把顶点的坐标代入即可求得a的值,从而求得抛物线C2的解析式;
a,由于CE⊥AB,所以直线CE的斜率为﹣2,进而求得直线CE为:y=﹣2x+a2﹣a,把顶点的坐标代入即可求得a的值,从而求得抛物线C2的解析式;
(3)PQ的长与C3移动到的位置无关,当抛物线C3的顶点在y轴时,抛物线的解析式为:y=x2﹣3,先求得直线l的解析式,然后与抛物线y=x2﹣3组成方程组,解方程组即可求得P、Q的横坐标,根据直线的斜率求得纵坐标的差等于横坐标差的一半,根据勾股定理即可求得PQ2 , 与已知条件PQ=3![]() 列出等式即可求得t的值;
列出等式即可求得t的值;


科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1050辆自行车,平均每天生产150辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比产量最少的一天多生产 辆;
(3)该厂实行计件工资制,每辆车50元,超额完成任务每辆奖10元,少生产一辆扣10元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)﹣7+13﹣6+20;
(2)3+(﹣2)﹣3×(﹣5)×0;
(3)16÷(﹣2)3﹣(﹣![]() )×(﹣4);
)×(﹣4);
(4)﹣36×(![]() );
);
(5)(2a2﹣1+2a)﹣(a﹣1+a2);
(6)8a+2b﹣2(5a﹣2b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简 [x]+(x)+[x)的结果是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某市8所学校抽取共1 000名学生进行800米跑达标抽样检测.结果显示该市达标学生人数超过半数,达标率达到52.5%.图l、图2反映的是本次抽样中的具体数据.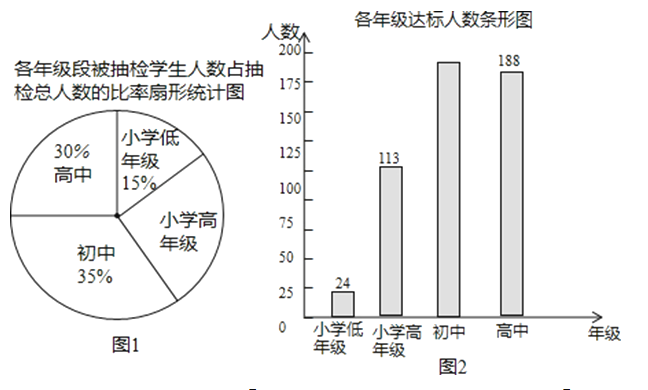
根据以上信息,下列判断:①小学高年级被抽检人数为200人;②小学、初中、高中学生中高中生800米跑达标率最大;③小学生800米跑达标率低于33%;④高中生800米跑达标率超过70%.其中判断正确的有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( )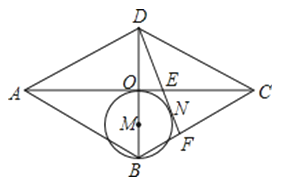
A.3
B.4
C.4.8
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】”4.20芦山地震”发生后,各地积极展开抗震救援工作,一支救援车队经过如图1所示的一座拱桥,拱桥的轮廓是抛物线型,拱高6m,跨度20m,相邻两支柱间的距离均为5m,将抛物线放在所给的直角坐标系中(如图2所示),拱桥的拱顶在y轴上.
(1)求拱桥所在抛物线的解析式;
(2)求支柱MN的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2米的隔离带),其中的一条行车道能否并排行驶宽2m、高2.4m的三辆汽车(隔离带与内侧汽车的间隔、汽车间的间隔、外侧汽车与拱桥的间隔均为0.5m)?请说说你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com