Question

设m为整数，且4＜m＜40，方程x²-2（2m-3）x+4m²-14m+8=0有两个不相等的整数根，求m的值及方程的根．

Answer 1

解：解方程x²-2（2m-3）x+4m²-14m+8=0，得，
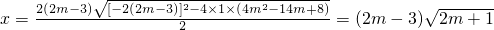
∵原方程有两个不相等的整数根，
∴2m+1为完全平方数，
又∵m为整数，且4＜m＜40，2m+1为奇数完全平方数，
∴2m+1=25或49，解得m=12或24．
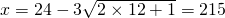
∴当m=12时，，x₁=26，x₂=16；
当m=24时，．
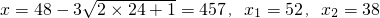
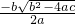
分析：根据求根公式可知：x==（2m-3）±，根据4＜m＜40可知m的值为12或24，再把m值代入求解即可．
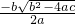
点评：本题考查了解一元二次方程的方法，求根公式法适用于任何一元二次方程．方程ax²+bx+c=0的解为x=．要注意根据实际意义进行值的取舍．