
【题目】在新冠病毒疫情防控期间,某校“停课不停学”,开展了网络教学.为了解九年级学生在网络学习期间英语学科和数学学科的学习情况,复课后从九年级学生中随机抽取60名学生进行了测试,获得了他们成绩(百分制)的数据,通过对成绩数据的整理、描述和分析,得到了如下部分信息.
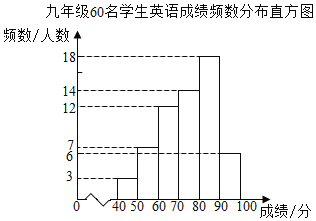
①英语成绩的频数分布直方图如图:
(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100.)
②英语和数学成绩的平均数、中位数、众数如表:
学科 | 平均数 | 中位数 | 众数 |
英语 | 74.8 | m | 83 |
数学 | 72.2 | 70 | 81 |
③英语成绩在70≤x<80这一组的数据是:
70 71 72 73 73 73 74 76 77 77 77 78 79 79
根据以上信息,回答下列问题:
(1)表中m的值是 .
(2)在此次测试中,李丽的英语成绩为74分,数学成绩为71分,该名学生成绩排名更靠前的学科是 .(填“英语”或“数学”),理由是 .
(3)若该校九年级共有500名学生,请你估计英语成绩超过77.5分的人数.
【答案】(1)76.5;(2)数学,该学生的成绩小于英语的中位数,而大于数学的中位数;(3)225人
【解析】
(1)根据统计图表求出总人数,判断中位数在70≤x<80这一组,根据中位数定义求解;
(2)可以从中位数角度进行分析;
(3)用样本的情况估计总体:英语成绩超过77.5分的人数为:500×![]() .
.
解:(1)∵英语成绩总人数为3+7+12+14+18+6=60,
∴中位数为第30、31个数据的平均数,而第30、31个数据均在70≤x<80这一组,
∴中位数在70≤x<80这一组,
∵70≤x<80这一组的是:70 71 72 73 73 73 74 76 77 77 77 78 79 79,
∴英语成绩的中位数为![]() =76.5,即m=76.5,
=76.5,即m=76.5,
故答案为:76.5;
(2)∵该学生的成绩小于英语成绩的中位数,而大于数学成绩的中位数,
∴这名学生成绩排名更靠前的课程是数学,
故答案为:数学,该学生的成绩小于英语的中位数,而大于数学的中位数;
(3)估计英语成绩超过77.5分的人数为500×![]() =225人.
=225人.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】九年级数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 120 | 160 | 190 |
月销售量y(件) | 260 | 180 | 120 |
月销售利润w(元) | 5200 | 10800 | 10800 |
注:月销售利润![]() 月销售量×(售价
月销售量×(售价![]() 进价)
进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围).
(2)求当售价为多少元时,月销售利润最大,并求最大利润是多少?
(3)由于某种原因,该商品进价降低了m元/件![]() ,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
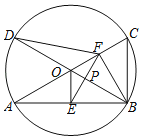
【题目】如图,已知AC,BD为⊙O的两条直径,连接AB,BC,OE⊥AB于点E,点F是半径OC的中点,连接EF.
(1)设⊙O的半径为1,若∠BAC=30°,求线段EF的长.
(2)连接BF,DF,设OB与EF交于点P,
①求证:PE=PF.
②若DF=EF,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
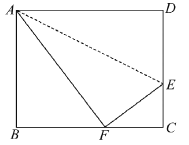
【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5![]() cm, 且tan∠EFC=
cm, 且tan∠EFC=![]() ,那么矩形ABCD的周长_____________cm.
,那么矩形ABCD的周长_____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
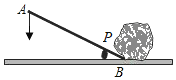
【题目】用杠杆撬石头的示意图如图所示,P是支点,当用力压杠杆的A端时,杠杆绕P点转动,另一端B向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的B端必须向上翘起8cm,已知杠杆的动力臂AP与阻力臂BP之比为4:1,要使这块石头滚动,至少要将杠杆的A端向下压_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆
O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆游泳的次数为![]() 次(
次(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
游泳次数 | 5 | 10 | 15 | … |
|
方式一的总费用(元) | 350 | 650 | … | ||
方式二的总费用(元) | 200 | 400 | … |
(2)若小亮计划今年游泳的总费用为2000元,选择哪种付费方式,他游泳的次数比较多;
(3)当![]() 时,小亮选择哪种付费方式更合算.并说明理由.
时,小亮选择哪种付费方式更合算.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
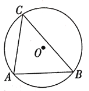
【题目】问题提出
(1)如图,![]() 是
是![]() 的弦,点
的弦,点![]() 是
是![]() 上的一点,在直线
上的一点,在直线![]() 上方找一点
上方找一点![]() ,使得
,使得![]() ,画出
,画出![]() ,并说明理由;
,并说明理由;
问题探究
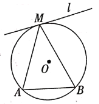
(2)如图,![]() 是
是![]() 的弦,直线
的弦,直线![]() 与
与![]() 相切于点
相切于点![]() ,点
,点![]() ,是直线
,是直线![]() 上异于点
上异于点![]() 的任意一点,请在图中画出图形,试判断
的任意一点,请在图中画出图形,试判断![]() 的大小关系;并说明理由;
的大小关系;并说明理由;
问题解决
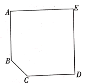
(3)如图,有一个平面图为五边形ABCDE的展览馆,其中![]() ,
,![]() ,
,![]() .展览馆保卫人员想在线段
.展览馆保卫人员想在线段![]() 上选一点
上选一点![]() 安装监控装置,用来监视边
安装监控装置,用来监视边![]() ,现只要使
,现只要使![]() 最大,就可以让监控装置的效果达到最佳,问在线段
最大,就可以让监控装置的效果达到最佳,问在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 最大?若存在,请求出符合条件的
最大?若存在,请求出符合条件的![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,且AB=4,点C是弧AB上的一动点(不与A,B重合),过点B作⊙O的切线交AC的延长线于点D,点E是BD的中点,连接EC.
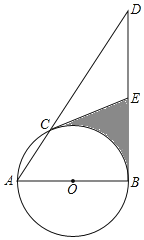
(1)若BD=8,求线段AC的长度;
(2)求证:EC是⊙O的切线;
(3)当∠D=30°时,求图中阴影部分面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com