【题目】如图，点
在线段
上，在的同侧作等腰
和等腰
，
与
、
分别交于点
、
.对于下列结论：
①
；②
；③
.其中正确的是（ ）
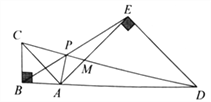
A. ①②③ B. ① C. ①② D. ②③
【答案】A
【解析】（1）由等腰Rt△ABC和等腰Rt△ADE三边份数关系可证；
（2）通过等积式倒推可知，证明△PAM∽△EMD即可；
（3）2CB2转化为AC2，证明△ACP∽△MCA，问题可证．
由已知：AC=
AB，AD=AE
∴
∵∠BAC=∠EAD
∴∠BAE=∠CAD
∴△BAE∽△CAD
所以①正确
∵△BAE∽△CAD
∴∠BEA=∠CDA
∵∠PME=∠AMD
∴△PME∽△AMD
∴
∴MPMD=MAME
所以②正确
∵∠BEA=∠CDA
∠PME=∠AMD
∴P、E、D、A四点共圆
∴∠APD=∠EAD=90°
∵∠CAE=180°-∠BAC-∠EAD=90°
∴△CAP∽△CMA
∴AC2=CPCM
∵AC=AB
∴2CB2=CPCM
所以③正确
故选A．
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）．
（1）请在图中，画出△ABC向左平移6个单位长度后得到的△A1B1C1；
（2）以点O为位似中心，将△ABC缩小为原来的
，得到△A2B2C2，请在图中y轴右侧，画出△A2B2C2，并求出∠A2C2B2的正弦值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在东西向的马路上有一个巡岗亭
，巡岗员从岗亭出发以
速度匀速来回巡逻，如果规定向东巡逻为正，向西巡逻为负，巡逻情况记录如下：（单位：千米）
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
（1）第几次结束时巡逻员甲距离岗亭最远？距离有多远？
（2）甲巡逻过程中配置无线对讲机，并一直与留守在岗亭的乙进行通话，问甲巡逻过程中，甲与乙保持通话的时长共多少小时？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知有理数a、b在数轴上的对应点如图所示．
（1）已知a=–2.3，b=0.4，计算|a+b|–|a|–|1–b|的值；
（2）已知有理数a、b，计算|a+b|–|a|–|1–b|的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校为了更新体育器材，计划购买足球和篮球共100个，经市场调查：购买2个足球和5个篮球共需600元；购买3个足球和1个篮球共需380元。
（1）请分别求出足球和篮球的单价；
（2）学校去采购时恰逢商场做促销活动，所有商品打九折，并且学校要求购买足球的数量不少于篮球数量的3倍，设购买足球a个，购买费用W元。
①写出W关于a的函数关系式，
②设计一种实际购买费用最少的方案，并求出最少费用。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知四边形ABCD是平行四边形，下列结论中，不一定正确的是（ ）
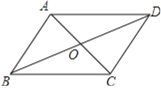
A.△AOB的面积等于△AOD的面积B.当AC⊥BD时，它是菱形
C.当OA=OB时，它是矩形D.△AOB的周长等于△AOD的周长
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】感知：解不等式 
．根据两数相除，同号得正，异号得负，得不等式组 
或不等式组
解不等式组 
，得 
；解不等式组 
，得 
，所以原不等式的解集为 或．
（1）探究：解不等式 
．
（2）应用：不等式 
的解集是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ABC=80°，∠BAC=40°.
（1）尺规作图作出AB的垂直平分线DE，分别与AC、AB交于点D、E．并连结BD；（保留作图痕迹，不写作法）
（2）证明：△ABC∽△BDC．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：
如图12-1，过锐角△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法：
，即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题：
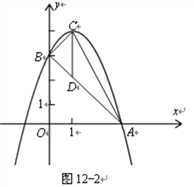
如图12-2，抛物线顶点坐标为点C(1，4)，交x轴于点A，交y轴于点B（0，3）.
(1)求抛物线解析式和线段AB的长度；
(2)点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及
；
(3)是否存在一点P，使S△PAB=
S△CAB，若存在，求出P点的坐标；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
