
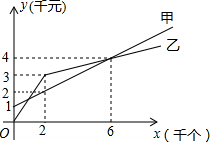
 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费分析 (1)当x=0时,y=1,由此即可得出甲厂的制版费为1千元,设y甲与x间的函数解析式为y甲=kx+b(k≠0),根据函数图象找出点的坐标,再利用待定系数法即可求出函数解析式;根据“单价=总价÷印刷数量”即可求出甲厂的印刷单价;
(2)设y乙与x间的函数解析式为y乙=mx+n(m≠0),观察函数图象找出点的坐标,利用待定系数法即可求出函数解析式,代入x=8,分别求出y甲与y乙的值,比较做差即可得出结论;
(3)结合(2)的结论,根据“减少的单价=减少费用÷印刷数量”算出结果即可.
解答 解:(1)当x=0时,y甲=1,
∴甲厂的制版费为1千元.
设y甲与x间的函数解析式为y甲=kx+b(k≠0),
将点(0,1)、(6,4)代入y甲=kx+b中,
得:$\left\{\begin{array}{l}{1=b}\\{4=6k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴y甲与x间的函数解析式为y甲=$\frac{1}{2}$x+1.
证书印刷单价为:(4-1)÷6=0.5(元/张).
答:甲厂的制版费为1千元,y甲与x间的函数解析式为y甲=$\frac{1}{2}$x+1,证书印刷单价为0.5元/张.
(2)设y乙与x间的函数解析式为y乙=mx+n(m≠0),
当x≥2时,将点(2,3)、(6,4)代入y乙=mx+n中,
得:$\left\{\begin{array}{l}{3=2m+n}\\{4=6m+n}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=\frac{1}{4}}\\{n=\frac{5}{2}}\end{array}\right.$,
∴y乙=$\frac{1}{4}$x+$\frac{5}{2}$.
当x=8时,y甲=$\frac{1}{2}$×8+1=5;
当x=8时,y乙=$\frac{1}{4}$×8+$\frac{5}{2}$=$\frac{9}{2}$.
∵5>$\frac{9}{2}$,且5-$\frac{9}{2}$=$\frac{1}{2}$(千元)=500(元).
∴当印制证书8千个时,选择乙厂,节省费用500元.
(3)每个证书降低费用为:500÷8000=$\frac{1}{16}$=0.0625(元).
答:如果甲厂想把8千个证书的印制费用不大于乙厂,在不降低制版费的前提下,每个证书最少降低0.0625元.
点评 本题考查了一次函数的应用以及利用待定系数法求函数解析式,解题的关键是:(1)(2)利用待定系数法求函数解析式;(3)根据数量关系直接计算.本题属于中档题,难度不大,但运算过程稍显繁琐,解决该题型题目时,根据函数图象找出点的坐标,再利用待定系数法求出函数解析式是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知某市2015年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2015年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,4,5 | B. | 7,24,25 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 2,3,4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com