
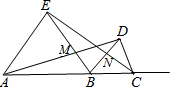
 如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是( )
如图,在△ABE和△BCD中,AB=BE=EA,BC=CD=DB,且两个三角形在线段AC同侧,则下列式子中错误的是( )| A、△ABD≌△EBC | B、△NBC≌△MBD | C、△ABM≌△EBN | D、△ABE≌△BCD |
|
|
|


科目:初中数学 来源: 题型:
 14、如图,在△ABE和△ACD中,AE=AD,添加一个条件
14、如图,在△ABE和△ACD中,AE=AD,添加一个条件查看答案和解析>>
科目:初中数学 来源: 题型:
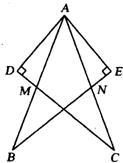 2、如图,在△ABE和△ACD中,给出以下四个论断:
2、如图,在△ABE和△ACD中,给出以下四个论断:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABE和△ACD中,给出以下四个论断:①AB=AC;②AD=AE;③AM=AN;④AD⊥DC,AE⊥BE.以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中,使其组成一个正确的命题.
如图,在△ABE和△ACD中,给出以下四个论断:①AB=AC;②AD=AE;③AM=AN;④AD⊥DC,AE⊥BE.以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中,使其组成一个正确的命题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com